题目内容
【题目】动手操作：（不要求写作法和证明，只保留作图痕迹）
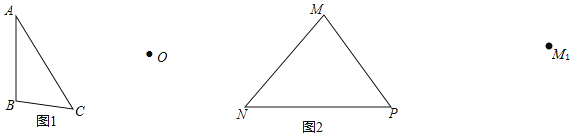
（1）如图
所示，以点
为对称中心，画出与
成中心对称的图形
．
（2）如图
所示，将
绕点
旋转后，顶点
旋转到了
处，试画出旋转后的
．
【答案】（1）如图所示，
即为所求；见解析；（2）如图所示，
即为所求；见解析．
【解析】
（1）依据中心对称的性质，分别连接AO并延长使A1O=AO，连接BO并延长使B1O=BO，连接CO并延长使C1O=CO，即可得到与△ABC成中心对称的图形△A1B1C1；
（2）依据旋转的方向，旋转角度以及旋转中心，连接PM1，作∠NPN1=∠MPM1，再在射线PN1上截取PN=PN1即可得到旋转后的△M1N1P．
解：（1）如图所示，△A1B1C1即为所求：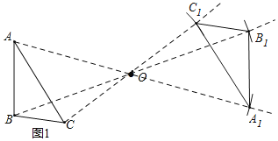
（2）如图所示，△M1N1P即为所求：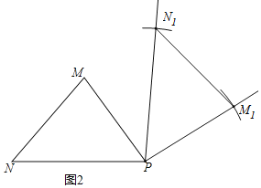
练习册系列答案
相关题目
【题目】如图所示，某学校有一边长为20米的正方形
区域（四周阴影是四个全等的矩形，记为区域甲；中心区是正方形
，记为区域乙）．区域甲建设成休闲区，区域乙建成展示区，已知甲、乙两个区域的建设费用如下表：
区域 | 甲 | 乙 |
价格（百元米2） | 6 | 5 |
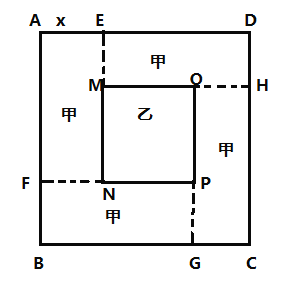
设矩形的较短边
的长为
米，正方形区域建设总费用为
百元．
（1）
的长为 米（用含的代数式表示）；
（2）求关于的函数解析式；
（3）当中心区的边长要求不低于8米且不超过12米时，预备建设资金220000元够用吗？请利用函数的增减性来说明理由．
