题目内容
【题目】在平面直角坐标系中,一次函数y![]() x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
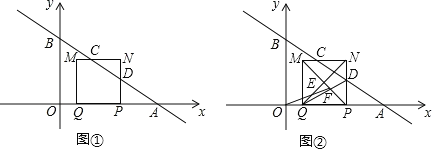
(1)当t=2秒时,OQ的长度为 ;
(2)设MN、PN分别与直线y![]() x+4交于点C、D,求证:MC=NC;
x+4交于点C、D,求证:MC=NC;
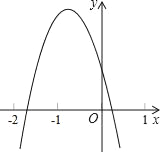
(3)在运动过程中,设正方形PQMN的对角线交于点E,MP与QD交于点F,如图2,求OF+EN的最小值.
【答案】(1)2;(2)证明见解析;(3)![]() .
.
【解析】
(1)解方程得到OA=6,由t=2,于是得到结论;
(2)根据AP=PQ=t,得到OQ=6-2t,根据正方形的性质得到PQ=QM=MN=PN=t,求得M(6-2t,t),N(6-t,t),C(6-![]() t,t),求得CM=(6-
t,t),求得CM=(6-![]() t)-(6-2t)=
t)-(6-2t)=![]() t,CN=(6-t)-(6-
t,CN=(6-t)-(6-![]() t)=
t)=![]() t,于是得到结论;
t,于是得到结论;
(3)作矩形NEFK,则EN=FK,推出当O,F,K三点共线时,OF+EN=OF+FK的值最小,如图,作OH⊥QN于H,解直角三角形即可得到结论.
(1)在y![]() x+4中,令y=0,得x=6,∴OA=6.
x+4中,令y=0,得x=6,∴OA=6.
∵t=2,∴AP=PQ=2,
∴OQ=6﹣2﹣2=2.
故答案为:2;
(2)∵AP=PQ=t,∴OQ=6﹣2t.
∵四边形PQMN是正方形,
∴PQ=QM=MN=PN=t,
∴M(6﹣2t,t),N(6﹣t,t),C(6![]() t,t),
t,t),
∴CM=(6![]() t)﹣(6﹣2t)
t)﹣(6﹣2t)![]() t,
t,
CN=(6﹣t)﹣(6![]() t)
t)![]() t,
t,
∴CM=CN;
(3)作矩形NEFK,则EN=FK.
∵OF+EN=OF+FK,
∴当O,F,K三点共线时,OF+EN=OF+FK的值最小,如图,
作OH⊥QN于H,
在等腰直角三角形PQN中,∵PQ=t,∴QN![]() t,
t,
∴HN=QN﹣QH![]() t﹣(
t﹣(![]() t﹣3
t﹣3![]() )=3
)=3![]() ,
,
∴OF+EN的最小值为:HE+EN=HN=3![]() .
.

【题目】某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名 | 黄瓜 | 茄子 |
批发价/(元/kg) | 2.4 | 2 |
零售价/(元/kg) | 3.6 | 2.8 |
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?