题目内容
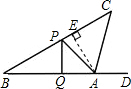
如图,小明同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小强同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
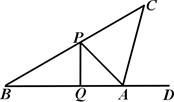
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC长约为多少?(结果保留根号)

(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC长约为多少?(结果保留根号)
(1)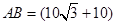 米;(2)
米;(2)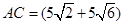 米
米
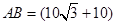 米;(2)
米;(2)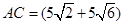 米
米试题分析:(1)在Rt△BPQ中,由∠B=30°,可得∠BPQ=60°,即可求得BQ的长,又在Rt△APQ中,∠PAB=∠APQ=45°,从而可求得AQ的长,即可得到结果;
(2)过A作AE⊥BC于E,在Rt△ABE中,可得AE的长,再在Rt△CAE中,即可得到结果.
(1)在Rt△BPQ中,PQ=10米,∠B=30°,
∴∠BPQ=90°-30°=60°,
则BQ=tan60°×PQ=
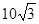 ,
,又在Rt△APQ中,∠PAB=∠APQ=45°,
则AQ=tan45°×PQ=10,
即:AB=(
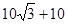 )(米);
)(米);(2)过A作AE⊥BC于E,
在Rt△ABE中,∠B=30°,AB=
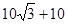 ,
,∴AE=sin30°×AB=
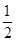 (
(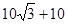 )=
)=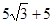 (米).
(米).∵∠CAD=75°,∠B=30°,
∴∠C=45°,
在Rt△CAE中,sin45°=
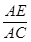 ,
,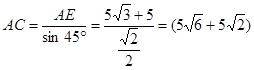 (米).
(米).点评:解答本题的关键是要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
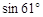 ≈0.87,
≈0.87,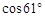 ≈0.48,
≈0.48, ≈1.80;
≈1.80;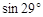 ≈0.48,
≈0.48,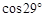 ≈0.87,
≈0.87, ≈0.55)
≈0.55)
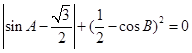 ,则这个三角形是( ).
,则这个三角形是( ).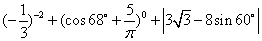 .
.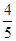 ,AB=10,则BC= .
,AB=10,则BC= .