题目内容
如图（1）、（2）中，（1）正方形A的面积为 .（2）斜边x= .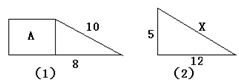
（1）36，（2）13
本题主要考查了勾股定理. （1）由勾股定理可求出正方形A的边长的平方，而正方形的面积=边长×边长，正好为所求出的值．（2）由勾股定理可得：斜边的平方=两直角边的平方和，将两直角边代入即可求出x的值．
解：（1）设A的边长为a，如图（1）所示：
在该直角三角形中，由勾股定理可得：
a2=102-82=36，
所以正方形A的面积为a2=36．
（2）如图（2）所示：
在该直角三角形中，由勾股定理可得：
x2=52+122，
所以，斜边x=13．
解：（1）设A的边长为a，如图（1）所示：
在该直角三角形中，由勾股定理可得：
a2=102-82=36，
所以正方形A的面积为a2=36．
（2）如图（2）所示：
在该直角三角形中，由勾股定理可得：
x2=52+122，
所以，斜边x=13．
练习册系列答案
相关题目
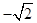的对应的点.(2分)
