题目内容
甲、乙两个港口相距72千米,一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,并立即返回(掉头时间忽略不计)。已知水流速度是2千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)

(1)轮船在静水中的速度是 千米/时;快艇在静水中的速度是 千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度)

(1)轮船在静水中的速度是 千米/时;快艇在静水中的速度是 千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
(1)22 ; 38(2)y=40x-160(4≤x≤5.8)(3)3小时或3.4小时
解:(1)22 ; 38。
(2)点F的横坐标为:4+72÷(38+2)="5.8" 。
∴F(5.8,72),E(4,0)。
设EF解析式为y=kx+b(k≠0),则
 ,解得
,解得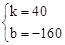 。
。
∴y=40x-160(4≤x≤5.8)。
(3)快艇出发3小时或3.4小时两船相距12千米。
(1)轮船在静水中的速度的=顺流速度-水流速度=72÷3-2=22千米/时;
快艇在静水中的速度=逆流速度+水流速度=72÷3+2=38千米/时。
(2)轮船回来时的速度是静水中的速度与水速的差,路程是两港口之间的距离,因而可以求得会来是所用的时间,则C的坐标可以求得,然后利用待定系数法即可求得函数的解析式。
(3)再求出函数EF的解析式,根据返回途中相距12千米,即两个函数的函数值的差是12,则可以列出方程,求得x的值:
轮船返回用时72÷(22-2)=3.6,∴点C的坐标为(7.6,0)。
设线段BC所在直线的解析式为y=kx+b,
∵经过点(4,72)(7.6,0),∴ ,解得:
,解得: 。
。
∴线段BC所在直线的解析式为:y=-20x+152。
根据题意得:40x-160-(-20x+152)=12或-20x+152-(40x-160)=12,
解得:x=5或x=5.4。
∵快艇在轮船出发2小时后从乙港出发,
∴快艇出发3小时或3.4小时两船相距12千米。
(2)点F的横坐标为:4+72÷(38+2)="5.8" 。
∴F(5.8,72),E(4,0)。
设EF解析式为y=kx+b(k≠0),则
 ,解得
,解得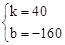 。
。∴y=40x-160(4≤x≤5.8)。
(3)快艇出发3小时或3.4小时两船相距12千米。
(1)轮船在静水中的速度的=顺流速度-水流速度=72÷3-2=22千米/时;
快艇在静水中的速度=逆流速度+水流速度=72÷3+2=38千米/时。
(2)轮船回来时的速度是静水中的速度与水速的差,路程是两港口之间的距离,因而可以求得会来是所用的时间,则C的坐标可以求得,然后利用待定系数法即可求得函数的解析式。
(3)再求出函数EF的解析式,根据返回途中相距12千米,即两个函数的函数值的差是12,则可以列出方程,求得x的值:
轮船返回用时72÷(22-2)=3.6,∴点C的坐标为(7.6,0)。
设线段BC所在直线的解析式为y=kx+b,
∵经过点(4,72)(7.6,0),∴
 ,解得:
,解得: 。
。 ∴线段BC所在直线的解析式为:y=-20x+152。
根据题意得:40x-160-(-20x+152)=12或-20x+152-(40x-160)=12,
解得:x=5或x=5.4。
∵快艇在轮船出发2小时后从乙港出发,
∴快艇出发3小时或3.4小时两船相距12千米。

练习册系列答案
相关题目
 的图象经过点A(0,-2),B(1,0),则b= ,k= .
的图象经过点A(0,-2),B(1,0),则b= ,k= . 小时后与北京的距离为
小时后与北京的距离为 千米,下列图象能大致反映
千米,下列图象能大致反映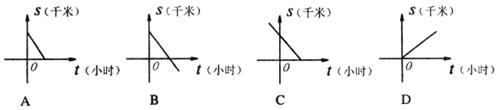
 (升)与时间
(升)与时间 (分钟)之间的关系如折线图所示:
(分钟)之间的关系如折线图所示:
 经过点A(
经过点A( ,
, )和点B(
)和点B( ),直线
),直线 经过点A,则不等式
经过点A,则不等式 的解集是
的解集是 

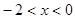



 经过A(-2,-1)、B(-3,0)两点,则不等式组
经过A(-2,-1)、B(-3,0)两点,则不等式组 的解集为 .
的解集为 .