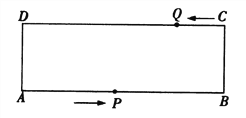
��Ŀ����
����Ŀ����ͼ����֪��B��1��3����C��1��0����ֱ��y=x+k������B������x�ύ�ڵ�A������ABC��ֱ��AB�۵��õ���ABD��
��1����գ�A������Ϊ�� �� ����D������Ϊ�� �� ����
��2����������y= ![]() x2+bx+c����C��D���㣬�������ߵĽ���ʽ��
x2+bx+c����C��D���㣬�������ߵĽ���ʽ��
��3������2���е���������y������ƽ�ƣ���ƽ�ƺ�������������y�ύ��ΪE����M��ƽ�ƺ����������ֱ��AB�Ĺ����㣬��������ƽ�ƹ������Ƿ����ijһλ��ʹ��ֱ��EM��x�ᣮ�����ڣ���ʱ����������ƽ���˼�����λ���������ڣ���˵�����ɣ�
����ʾ��������y=ax2+bx+c��a��0���ĶԳ�����x=�� ![]() �����������ǣ���
�����������ǣ��� ![]() ��
�� ![]() ��
��
���𰸡�
��1����2��0����2��3
��2��
�⣺��������y= ![]() x2+bx+c����C��1��0����D����2��3�����룬��ã�b=��
x2+bx+c����C��1��0����D����2��3�����룬��ã�b=�� ![]() ��c=
��c= ![]()
�����������߽���ʽΪ��y= ![]() x2��
x2�� ![]() x+
x+ ![]() ��
��
��3��
�⣺�𣺴��ڣ�
�ߵ���M�������߶Գ���������������ߵĶ���ʱ������M��E�غ�ʱ�����ǵ���������ȣ�
��EM������x��ƽ�У�
����M�������ߵ��Ҳ�ʱ��
������������ƽ��H����λ��ʹEM��x�ᣬ
��ƽ�ƺ�������ߵĽ���ʽΪ
��y= ![]() ��x��1��2+h��
��x��1��2+h��
����������y�ύ��E��0�� ![]() +h����
+h����
�������ߵĶԳ���Ϊ��x=1��
���������ߵĶԳ��ԣ���֪��M������Ϊ��2�� ![]() +h��ʱ��ֱ��EM��x�ᣬ
+h��ʱ��ֱ��EM��x�ᣬ
����2�� ![]() +h������y=x+2��
+h������y=x+2�� ![]() +h=2+2
+h=2+2
��ã�h= ![]() ��
��
������������ƽ�� ![]() ����λ��ʹEM��x�ᣮ
����λ��ʹEM��x�ᣮ
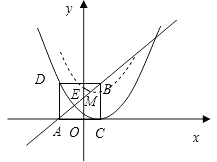
���������⣺��1��A����2��0����D����2��3��
�����㾫����������Ĺؼ�����������κ�����ͼ������֪ʶ�����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣬�Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��