题目内容
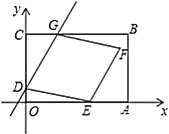
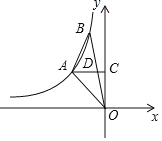
【题目】如图,A、B是反比例函数![]() 图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
【答案】![]()
【解析】
过B作BE⊥y轴于E,得到CD∥BE,根据三角形中位线的性质得到CD=![]() BE,于是得到S△OBE=4S△OCD=
BE,于是得到S△OBE=4S△OCD=![]() ,求得S△OAD=2,根据反比例函数的系数k的几何意义得到S△OCD=
,求得S△OAD=2,根据反比例函数的系数k的几何意义得到S△OCD=![]() ,建立方程即可求出k的值.
,建立方程即可求出k的值.
如图所示,过B作BE⊥y轴于E,

∵BE⊥y轴,AC⊥y轴,
∴CD∥BE,
∵D为OB的中点,
∴CD为△OBE的中位线,
∴CD=![]() BE,
BE,
∴S△OBE=4S△OCD=![]() ,
,
∴S△OCD=![]()
∵△ABO的面积为4,D为OB的中点,
∴S△OAD=2,
∵S△AOC=![]() ,
,
∴S△OCD=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 | 86 | 92 | 80 | 90 |
面试 | 90 | 88 | 94 | 84 |
(1)这4名选手笔试成绩的中位数是 分,面试的平均数是 分.
(2)该公司规定:笔试、面试分别按40%,60%的比例计入总分,且各项成绩都不得低于85分. 根据规定,请你说明谁将被录用.