��Ŀ����
����Ŀ�������ⷢ�֣�
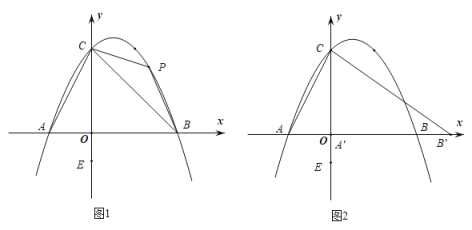
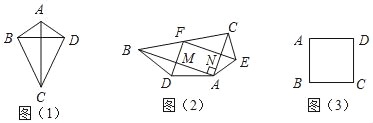
��1����ͼ��1���ı���ABCD�У���AB=AD��CB=CD�����߶�BD��AC��λ�ù�ϵΪ�� ����
����չ̽����
��2����ͼ��2����Rt��ABC�У���FΪб��BC���е㣬�ֱ���AB��ACΪ�ױߣ���Rt��ABC�ⲿ������������ABD�͵���������ACE������FD��FE���ֱ�AB��AC�ڵ�M��N���Բ����ı���FMAN����״����˵�����ɣ�
��������⣩
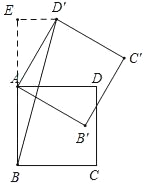
��3����ͼ��3����������ABCD�У�AB=2![]() ���Ե�AΪ��ת���Ľ�������ABCD��ת60�����õ�������AB'C'D'����ֱ��д��BD'ƽ����ֵ��
���Ե�AΪ��ת���Ľ�������ABCD��ת60�����õ�������AB'C'D'����ֱ��д��BD'ƽ����ֵ��
���𰸡���1��AC��ֱƽ��BD����2���ı���FMAN�Ǿ��Σ����ɼ���������3��16+8![]() ��16��8
��16��8![]()
��������
��1�����ݵ�A���߶�BD�Ĵ�ֱƽ�����ϣ���C���߶�BD�Ĵ�ֱƽ�����ϣ����ɵó�AC��ֱƽ��BD��
��2������Rt��ABC�У���FΪб��BC���е㣬�ɵ�AF=CF=BF���ٸ��ݵ���������ABD �͵���������ACE�����ɵõ�AD=DB��AE=CE�������ó���AMF=��MAN=��ANF=90���������ж��ı���AMFN�Ǿ��Σ�
��3����������������Ե�AΪ��ת���Ľ�������ABCD��ʱ����ת60�㣬���Ե�AΪ��ת���Ľ�������ABCD˳ʱ����ת60�����ֱ�������ת�������Լ����ɶ��������ɵõ����ۣ�
��1����AB=AD��CB=CD��
���A���߶�BD�Ĵ�ֱƽ�����ϣ���C���߶�BD�Ĵ�ֱƽ�����ϣ�
��AC��ֱƽ��BD��
�ʴ�Ϊ��AC��ֱƽ��BD��
��2���ı���FMAN�Ǿ��Σ����ɣ�
��ͼ2������AF��
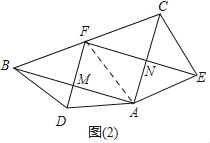
��Rt��ABC�У���FΪб��BC���е㣬
��AF=CF=BF��
�֡ߵ���������ABD �͵���������ACE��
��AD=DB��AE=CE��
���ɣ�1���ɵã�DF��AB��EF��AC��
�֡ߡ�BAC=90�㣬
���AMF=��MAN=��ANF=90�㣬
���ı���AMFN�Ǿ��Σ�
��3��BD����ƽ��Ϊ16+8![]() ��16��8
��16��8![]() ��
��
�����������
���Ե�AΪ��ת���Ľ�������ABCD��ʱ����ת60�㣬
��ͼ��ʾ����D'��D'E��AB����BA���ӳ�����E��
����ת�ɵã���DAD'=60�㣬
���EAD'=30�㣬
��AB=2![]() =AD'��
=AD'��
��D'E=![]() AD'=
AD'=![]() ��AE=
��AE=![]() ��
��
��BE=2![]() +
+![]() ��
��
��Rt��BD'E��BD'2=D'E2+BE2=��![]() ��2+��2
��2+��2![]() +
+![]() ��2=16+8
��2=16+8![]()
���Ե�AΪ��ת���Ľ�������ABCD˳ʱ����ת60�㣬
��ͼ��ʾ����B��BF��AD'��F��

��ת�ɵã���DAD'=60�㣬
���BAD'=30�㣬
��AB=2![]() =AD'��
=AD'��
��BF=![]() AB=
AB=![]() ��AF=
��AF=![]() ��
��
��D'F=2![]() ��
��![]() ��
��
��Rt��BD'F��BD'2=BF2+D'F2=��![]() ��2+��2
��2+��2![]() -
-![]() ��2=16��8
��2=16��8![]()
����������BD��ƽ���ij���Ϊ16+8![]() ��16��8
��16��8![]() ��
��

����Ŀ��ij��ѧ��ʦΪ���˽�ѧ������ѧѧϰ�г�������ľ���������ռ�������ѧ������ҵ�Ϳ����еij�����������10��ѡ���⣬ÿ��3�֣��������̵ij�����1���ࡢ��2��������˼�⣬��ͼ��ʾ������������ȡ��10��ѧ���ĵ÷����.
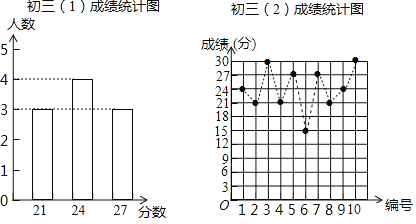
��1������ͼ���ṩ����Ϣ����ȫ�±���
�༶ | ƽ����/�� | ��λ��/�� | ����/�� |
������1���� | __________ | 24 | ________ |
������2���� | 24 | _________ | 21 |
��2������24�����ϣ���24�֣���Ϊ���������������40��ѧ���������������ж�����ѧ���ɼ����㣻
��3���۲���ͼ�����ݷֲ��������ͨ������˵���ĸ����ѧ�������ĵ÷ָ��ȶ���