Question

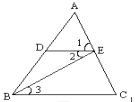
【题目】（2016浙江省丽水市）如图，在菱形ABCD中，过点B作BE⊥AD，BF⊥CD，垂足分别为点E，F，延长BD至G，使得DG=BD，连结EG，FG，若AE=DE，则=____．

Answer 1

【答案】．

【解析】如图，连接AC、EF，在菱形ABCD中，AC⊥BD，∵BE⊥AD，AE=DE，∴AB=BD，

又∵菱形的边AB=AD，∴△ABD是等边三角形，∴∠ADB=60°，

设EF与BD相交于点H，AB=4x，∵AE=DE，∴由菱形的对称性，CF=DF，∴EF是△ACD的中位线，∴DH=DO=BD=x，

在Rt△EDH中，EH=DH=x，

∵DG=BD，∴GH=BD+DH=4x+x=5x，

在Rt△EGH中，由勾股定理得，EG===，

所以，==，

故答案为：．