题目内容
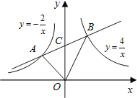
【题目】如图①,直线![]() 与
与![]() 轴负半轴、
轴负半轴、![]() 轴正半轴分别交于
轴正半轴分别交于![]() 两点,
两点,![]() 的长度分别为
的长度分别为![]() 和
和![]() ,且满足
,且满足![]() .
.
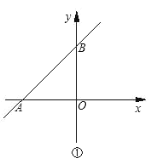
(1)![]() 是________三角形.
是________三角形.
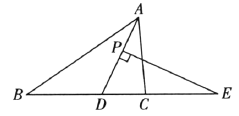
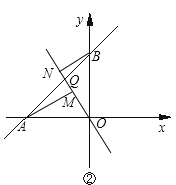
(2)如图②,正比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() ,过
,过![]() 两点分别作
两点分别作![]() 于
于![]() ,
,![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
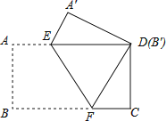
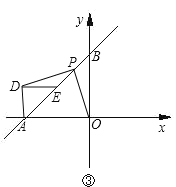
(3)如图③,![]() 为
为![]() 上一动点,以
上一动点,以![]() 为斜边作等腰直角
为斜边作等腰直角![]() ,
,![]() 为
为![]() 的中点,连
的中点,连![]() ,试问:线段
,试问:线段![]() 是否存在某种确定的数量关系和位置关系?写出你的结论并说明理由.
是否存在某种确定的数量关系和位置关系?写出你的结论并说明理由.
【答案】(1)等腰直角;(2)6;(3)PO=PD且PO⊥PD.理由见解析.
【解析】
(1)已知a2-2ab+b2=0,化简可得a=b,然后可得△AOB为等腰直角三角形;
(2)证明△MAO≌△NOB,得出AM=ON,然后求出MN的值;
(3)根据已知E为中点,联想到延长DP到点C,使DP=PC,再连接OD、OC、BC,先证明△DEP≌△CBP得到边角的等量关系,再证明△OAD≌△OBC,最后可得出△DOC为等腰直角三角形,从而得出结论.
解:(1)∵a2-2ab+b2=0,∴(a-b)2=0,
∴a=b,
∵∠AOB=90°,
∴△AOB为等腰直角三角形.
故答案为:等腰直角;
(2)∵∠MOA+∠MAO=90°,∠MOA+∠MOB=90°,
∴∠MAO=∠MOB,
∵AM⊥OQ,BN⊥OQ,
∴∠AMO=∠BNO=90°,
在△MAO和△BON中,
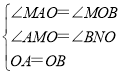 ,
,
∴△MAO≌△NOB(AAS),
∴AM=ON,
∴MN=ON-OM=AM-OM=6;
(3)PO=PD且PO⊥PD.理由如下:
如图,延长DP到点C,使DP=PC,连接OD、OC、BC,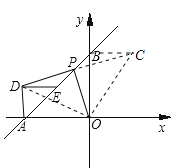
在△DEP和△CBP,
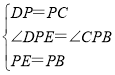 ,
,
∴△DEP≌△CBP(SAS),
∴CB=DE=DA,∠DEP=∠CBP=135°,
则∠CBO=∠CBP-∠ABO=135°-45°=90°,
又∵∠BAO=45°,∠DAE=45°,
∴∠DAO=90°,
在△OAD和△OBC,
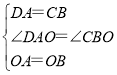 ,
,
∴△OAD≌△OBC(SAS),
∴OD=OC,∠AOD=∠COB,
∴∠COD=∠AOB=90°,
∴△DOC为等腰直角三角形,
∴PO=PD,且PO⊥PD.