题目内容
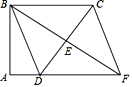
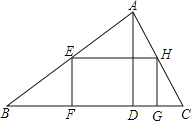
【题目】如图,△ABC中,∠C=90°,AC=6,BC=![]() ,点E从A出发沿线段AC运动至点C停止,ED⊥AB,EF⊥AC,将△ADE沿直线EF翻折得到△A′D′E,设DE=x,△A′D′E与△ABC重合部分的面积为y.
,点E从A出发沿线段AC运动至点C停止,ED⊥AB,EF⊥AC,将△ADE沿直线EF翻折得到△A′D′E,设DE=x,△A′D′E与△ABC重合部分的面积为y.
(1)当x= 时,D′恰好落在BC上?
(2)求y关于x的函数关系式,并写出x的取值范围.

【答案】(1)![]() ;
;
(2)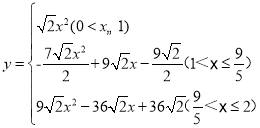 .
.
【解析】
(1)先根据勾股定理求出AB的值,然后根据同角的正弦函数值相等表示出AE为3x,当点D′恰好落在BC上时,再根据等角的三角函数值相等表示出EC为![]() ,然后求出x的值即可;
,然后求出x的值即可;
(2)由(1)可得AE和AD,当点A'与点C重合时,求出x的值,然后根据三角形的面积公式分三种情况讨论,求出y关于x的函数关系式即可.
解:(1)在Rt△ABC中,AB=![]() ,
,
∴sinA=![]() ,
,
∵DE=x,
∴AE=3x,
当D′恰好落在BC上时,如图所示:
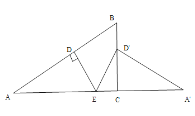
ED′=ED=x,∠DEA=∠D′EC,
∴∠ED′C=∠A,
∴EC=![]() x,
x,
∵3x+![]() x=6,
x=6,
∴x=![]() ,
,
故答案为:![]() ;
;
(2)由(1)可得,AE=3x,
∴AD=![]() ,
,
当点A'与点C重合时,AE=EC=![]() AC=3,
AC=3,
∴3x=3
∴x=1.
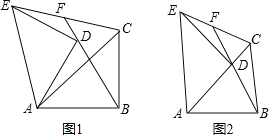
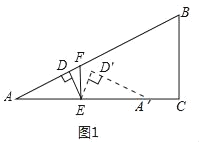
①当0<x≤1时,如图1,y=![]()
![]() ;
;
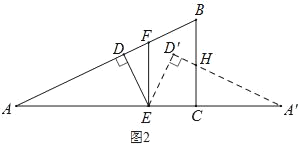
②当1<x≤![]() 时,如图2,
时,如图2,
∵AE=A'E=3x,
∴AA'=6x.
∴CA'=6x﹣6.
∵tan A'![]() ,
,
∴![]() ,
,
∴y=![]()
=-![]() ;
;
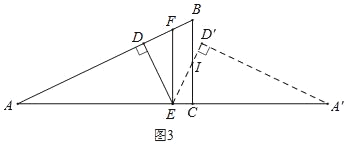
③当![]() 时,如图3,
时,如图3,
∵∠EIC+∠IEC=∠IEC+∠A',
∴∠EIC=∠A'.
∴![]() ,
,
∵CE=(6﹣3x),
∴![]()
∴![]()
=![]()
综上所述,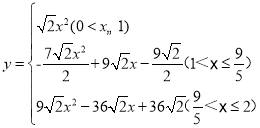 .
.

 云南师大附小一线名师提优作业系列答案
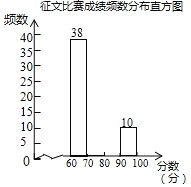
云南师大附小一线名师提优作业系列答案【题目】今年我区作为全国作文教学改革试验区,举办了中小学生现场作文大赛,全区七、八年级的学生参加了中学组的比赛,大赛组委会对参赛获奖作品的成绩进行统计,每篇获奖作品成绩为m分(60≤m≤100)绘制了如下两幅数据信息不完整的统计图表.
获奖作品成绩频数分布表
分数段 | 频数 | 频率 |
60≤x<70 | 38 | 0.38 |
70≤x<80 | a | 0.32 |
80≤x<90 | b | |
90≤x<100 | 10 | |
合计 | 1 |
请根据以上信息,解决下列问题:
(1)获奖作品成绩频数分布表中a= ,b= ;
(2)把获奖作品成绩频数分布直方图缺失的信息补全;
(3)某校八年级二班有两名男同学和两名女同学在这次大赛中获奖,并且其中两名同学获得了大赛一等奖,请用列表或画树状图法求出恰好一男一女获得一等奖的概率.