Question

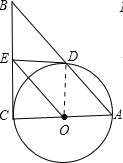
【题目】如图，AB，AC均为⊙O的切线，切点分别为B，C，点D是优弧BC上一点，则下列关系式中，一定成立的是（　　）

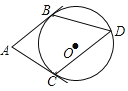
A. ∠A+∠D＝180°B. ∠A+2∠D＝180°

C. ∠B+∠C＝270°D. ∠B+2∠C＝270°

Answer 1

【答案】B

【解析】

连接OB，OC，由AB与AC为圆O的切线，根据切线的性质以及四边形的内角和为360度可对选项A、B作出判断；连接OB、BC，OC，延长BO交圆于E，连接DE，根据直径所对的圆周角是直角，可求得∠DBE+∠E＝90°，继而通过角的代换可得∠ABO+∠DBE+∠BCD+∠ACO＝270°，再根据∠ACB＜∠ACO，继而可得∠ABD+∠ACD＜270°，∠ABD+∠ACD+∠OCB＝270°，由此即可判断C、D选项.

连接OB，OC，如图1所示：

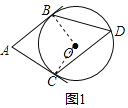
∵AB，AC分别为圆O的切线，

∴AB⊥OB，AC⊥OC，

∴∠ABO＝∠ACO＝90°，

∴∠A+∠BOC＝360°﹣(∠ABO+∠ACO)＝180°，

∵∠BOC＝2∠D，

∴∠A+2∠D＝180°，故A不成立，B成立；

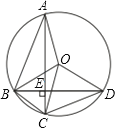
②连接OB、BC，OC，延长BO交圆于E，如图2所示：

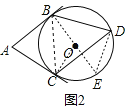
∵BE是直径，

∴∠BDE＝90°，

∴∠DBE+∠E＝90°，

∵∠ABO＝∠ACO＝90°，∠E＝∠BCD，

∴∠ABO+∠DBE+∠BCD＝180°，

∴∠ABO+∠DBE+∠BCD+∠ACO＝270°，

∵∠ACB＜∠ACO，

∴∠ABO+∠DBE+∠BCD+∠ACB＜270°，

即∠ABD+∠ACD＜270°，∠ABD+∠ACD+∠OCB＝270°，

∵∠OCB＜∠ACD，故C、D都不成立，

故选B．