题目内容
【题目】在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=![]() ,则称点Q为点P的“可控变点”.请问:若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的值是____.
,则称点Q为点P的“可控变点”.请问:若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的值是____.
【答案】4![]() .
.
【解析】
根据新定义,分析函数y=-x2+16在新定义下点P的“可控变点”横坐标与纵坐标的对应关系,在分析a的取值范围.
由定义可知:
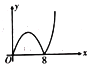
①当0≤x≤a时,y′=﹣x2+16,此时,抛物线y′的开口向下,故当0≤x≤a时,y′随x的增大而减小(如图)

即:﹣a2+16≤y′≤16,
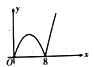
②当﹣5≤x<0时,y′=x2﹣16,抛物线y′的开口向上,故当﹣5≤x<0时,y′随x的增大而减小(如图),
即:﹣16<y′≤9,
∵点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,
∴﹣a2+16≥﹣16
∴a2≤32,
∴﹣4![]() ≤a≤4
≤a≤4![]() ,
,
又∵﹣5≤x≤a,
∴a=4![]() ,
,
在函数y=﹣x2+16图象上的点P,当a=4![]() 时,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,
时,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,
故答案为4![]() .
.

练习册系列答案
相关题目