题目内容
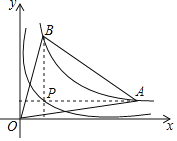
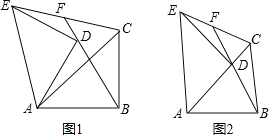
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转,得到△ADE,旋转角为α(0°<α<90°),连接BD交CE于点F.
(1)如图2,当α=45°时,求证:CF=EF;
(2)在旋转过程中,①问(1)中的结论是否仍然成立?证明你的结论;②连接CD,当△CDF为等腰直角三角形时,求tan![]() 的值.
的值.
【答案】(1)见解析;(2) ① 成立,理由见解析;②![]()
【解析】
(1)如图中,由∠EAC=∠DAB,AE=AC,AD=AB,可得∠AEC=∠ACE=∠ADB=∠ABD,继而可得FD=FC,再根据∠EDC=90°,继而可推导得出∠FED=∠FDE,可得FE=FD,即可求得EF=FC;
(2)①如图1中,结论仍然成立.理由:连接AF,由旋转的性质可推导得出∠FCA=∠ABF,从而可得A,B,C,F四点共圆,继而根据圆内接四边形的性质可求得∠AFC=90°,有AF⊥EC,再根据AE=AC,即可求得EF=CF;
②分CF=CD,∠FCD=90°和DF=DC,∠CDF=90°两种情况分别进行讨论即可得.
(1)如图中,

∵∠EAC=∠DAB,AE=AC,AD=AB,
∴∠AEC=∠ACE=∠ADB=∠ABD,
∵∠ADB=∠CDF,
∴∠FDC=∠FCD,
∴FD=FC,
∵∠EDC=90°,
∴∠DEF+∠ECD=90°,∠FDE+∠FDC=90°,
∴∠FED=∠FDE,
∴FE=FD,
∴EF=FC.
(2)①如图1中,结论仍然成立.
理由:连接AF.

∵AB=AD,AE=AC,
∴∠ABD=∠ADB,∠ACE=∠EAC,
又∵∠BAD=∠CAE,∠ABD+∠ADB+∠BAD=180°,∠ACE+∠EAC+∠CAE=180°,
∴∠FCA=∠ABF,
∴A,B,C,F四点共圆,
∴∠AFC+∠ABC=180°,
∵∠ABC=90°,
∴∠AFC=90°,
∴AF⊥EC,
∵AE=AC,
∴EF=CF.
②如图3﹣1中,当CF=CD,∠FCD=90°时,连接AF,作CH⊥BF于H.设CF=CD=a.

则DE=![]() ,DF=
,DF=![]() a,
a,
∵CF=CD,CH⊥DF,
∴HF=HD,
∴CH=![]() DF=
DF=![]() a,
a,
∴BC=DE=![]() a,
a,
∴BH=![]() ,
,
∵AE=AC,EF=CF,
∴AF平分∠EAC,
∵A,B,C,F四点共圆,
∴∠CAF=∠CBH=![]() α,
α,
∴tan![]() α=
α=![]() =
= ;
;
如图3﹣2中,当DF=DC,∠CDF=90°时,作DH⊥CF于H,连接AF.设CD=DF=m.

则CF=EF=![]() a,DH=
a,DH=![]() CF=
CF=![]() m,
m,
∴DE=BC=![]() m,
m,
∴BD=![]() =2m,
=2m,
∴tan![]() α=
α=![]() =
=![]() .
.

【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?