题目内容
【题目】定义:在平面直角坐标系中,图形G上点P![]() 的纵坐标
的纵坐标![]() 与其横坐标
与其横坐标![]() 的差
的差![]() 称为P点的“坐标差”,记作Zp,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
称为P点的“坐标差”,记作Zp,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)①点A(3,1)的“坐标差”为 ;
②求抛物线![]() 的“特征值”;
的“特征值”;
(2)某二次函数![]() 的“特征值”为
的“特征值”为![]() ,点B
,点B![]() ,
,![]() 与点C分别是此二次函数的图象与
与点C分别是此二次函数的图象与![]() 轴和
轴和![]() 轴的交点,且点B与点C的“坐标差”相等.
轴的交点,且点B与点C的“坐标差”相等.
①直接写出![]() ;(用含
;(用含![]() 的式子表示)
的式子表示)
②求此二次函数的表达式.
【答案】(1)①![]() ;②抛物线
;②抛物线![]() 的“特征值”为4;(2)①
的“特征值”为4;(2)①![]() ;②
;②![]() .
.
【解析】
(1)①由“坐标差”的定义可求出点A(3,1)的“坐标差”;
②用y-x可找出y-x关于x的函数关系式,再利用配方法即可求出y-x的最大值,进而可得出抛物线y=-x![]() +5x的“特征值”;
+5x的“特征值”;
(2)①利用二次函数图象上点的坐标特征可求出点C的坐标,由“坐标差”的定义结合点B与点C的“坐标差"相等,即可求出m的值;
②由点B的坐标利用待定系数法可找出b,c之间的关系,找出y-x关于x的函数关系式,再利用二次函数的性质结合二次函数y=-x![]() +bx+c(c≠0)的“特征值"为-1,即可得出关于b的一元二次方程,解之即可得出b的值,进而可得出c的值,此问得解;
+bx+c(c≠0)的“特征值"为-1,即可得出关于b的一元二次方程,解之即可得出b的值,进而可得出c的值,此问得解;
解:(1)①![]()
②![]() ,
,
∵![]() ,
,
∴当![]() 时,y-x取得最大值,最大值为4.
时,y-x取得最大值,最大值为4.
∴抛物线![]() 的“特征值”为4.
的“特征值”为4.
(2)①-c
②由①可知:点B的坐标为![]() ,
,![]() .
.
将点B![]() ,
,![]() 代入
代入![]() ,得:
,得:![]() ,
,
∴![]() (舍去).
(舍去).
∵二次函数![]() 的“特征值”为
的“特征值”为![]() ,
,
∴![]() 的最大值为
的最大值为![]() ,
,
∴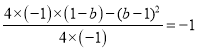 ,
,
解得:![]() ,
,
∴![]() ,
,
∴二次函数的解析式为![]() .
.

练习册系列答案
相关题目