题目内容
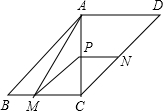 如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发沿AC向终点C移动,过点P分别作PM∥AB交BC于M,PN∥AD交DC于N.连接AM.设AP=x
如图,在?ABCD中,对角线AC⊥BC,AC=BC=2,动点P从点A出发沿AC向终点C移动,过点P分别作PM∥AB交BC于M,PN∥AD交DC于N.连接AM.设AP=x
(1)四边形PMCN的形状有可能是菱形吗?请说明理由;
(2)当x为何值时,四边形PMCN的面积与△ABM的面积相等?
解:(1)四边形PMCN不可能是菱形.
点P在运动过程中,△PCM始终是一个直角三角形
斜边PM大于直角边MC
∴四边形PMCN不可能是菱形
(2)∵AC=BC=2,AB∥PM,
∴AP=BM=x,
∴S△ABM= ×BM×AC=
×BM×AC= ×x×2=x,
×x×2=x,
∵由巳知可得四边形PMCN是平行四边形,
∴S四边形PMCN=MC•PC=(2-x)2
解得x1=1,x2=4
x2=4不符合题意,舍去
当x=1时,四边形PMCN的面积与△ABM的面积相等.
分析:(1)由题可知,四边形PMCN是一个?,而要想成为一个菱形,则必须有邻边相等,如PM=MC,而PM和MC同在一直角三角形中,且PM为斜边>直角边MC,因此不会为菱形;
(2)S△ABM=x,由巳知可得四边形PMCN是平行四边形,则S四边形PMCN=(2-x)2
解得x1=1,x2=4而x2=4不符合题意,舍去∴当x=1时,四边形PMCN的面积与△ABM的面积相等.
点评:此题主要考查了平行四边形和菱形的概念和性质,难易程度适中.
点P在运动过程中,△PCM始终是一个直角三角形
斜边PM大于直角边MC
∴四边形PMCN不可能是菱形
(2)∵AC=BC=2,AB∥PM,
∴AP=BM=x,
∴S△ABM=
 ×BM×AC=
×BM×AC= ×x×2=x,
×x×2=x,∵由巳知可得四边形PMCN是平行四边形,
∴S四边形PMCN=MC•PC=(2-x)2
解得x1=1,x2=4

x2=4不符合题意,舍去
当x=1时,四边形PMCN的面积与△ABM的面积相等.
分析:(1)由题可知,四边形PMCN是一个?,而要想成为一个菱形,则必须有邻边相等,如PM=MC,而PM和MC同在一直角三角形中,且PM为斜边>直角边MC,因此不会为菱形;
(2)S△ABM=x,由巳知可得四边形PMCN是平行四边形,则S四边形PMCN=(2-x)2
解得x1=1,x2=4而x2=4不符合题意,舍去∴当x=1时,四边形PMCN的面积与△ABM的面积相等.
点评:此题主要考查了平行四边形和菱形的概念和性质,难易程度适中.

练习册系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=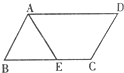 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.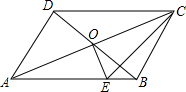 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是