题目内容
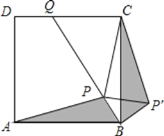
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为![]() ,1,2
,1,2![]() ,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
【答案】45
【解析】
△ABP绕点B旋转90°至△CBP′,可知∠PBP′=90°,BP′=BP故可求出PP′=![]() =
=![]() ,又△ABP≌△CBP′得CP′=AP=
,又△ABP≌△CBP′得CP′=AP=![]() ,故可利用勾股定理逆定理知△CPP′是直角三角形,得∠CPP′=90°,即可求出∠CPQ.
,故可利用勾股定理逆定理知△CPP′是直角三角形,得∠CPP′=90°,即可求出∠CPQ.
△ABP绕点B旋转90°至△CBP′,
∴∠PBP′=90°,BP′=BP
∴PP′=![]() =
=![]() ,
,
又△ABP≌△CBP′
则CP′=AP=![]() ,
,
又CP=2![]() ,PP′=
,PP′=![]()
∴CP′=CP+PP′,
∴△CPP′是直角三角形,得∠CPP′=90°,
∴∠CPQ=180°-∠CPP′-∠P′PB=45°

练习册系列答案
相关题目