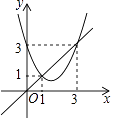题目内容
【题目】完成下面的证明.
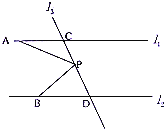
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

【答案】详见解析.
【解析】
试题因为AB∥CD,由此得到∠4=∠BAF,它们是同位角,由此得到根据两直线平行,同位角相等;
由∠4=∠BAF,∠3=∠4得到∠3=∠BAF的根据是等量代换;
由∠BAF=∠CAD和已知结论得到∠3=∠CAD的根据是等量代换;
由∠3=∠CAD得到AD∥BE的根据是内错角相等,两直线平行.
∵AB∥CD(已知),
∴∠4=∠BAF(两直线平行,同位角相等).
∵∠3=∠4(已知),
∴∠3=∠BAF(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质),
即∠BAF=∠CAD.
∴∠3=∠CAD(等量代换).
∴AD∥BE(内错角相等,两直线平行).

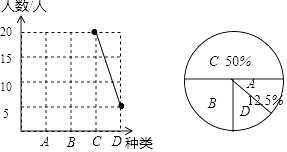
【题目】“戒烟一小时,健康亿人行”,今年国际无烟日,某市团委组织人员就公众对在超市吸烟的态度进行了随机抽样调查,主要由四种态度:A.顾客出面制止;B.劝说进吸烟室;C.超市老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:
态度 | A.顾客出面制止 | B.劝说进吸烟室 | C.超市老板出面制止 | D.无所谓 |
频数(人数) | 90 | 30 | 10 |
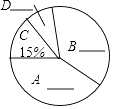
请你根据统计图、表提供的信息解答下列问题:
(1)这次抽样的公众有人.
(2)请将统计表和扇形统计图补充完整;
(3)在统计图中“B”部分所对应的圆心角是度.
(4)若该市有120万人,估计该市态度为“A.顾客出面制止”的有万人.