题目内容
【题目】如图为K90的化学赛道,其中助滑坡AB长90米,坡角a=40°,一个曲面平台BCD连接了助滑坡AB与着陆坡,某运动员在C点飞向空中,几秒之后落在着陆坡上的E处,已知着陆坡DE的坡度i=1: ![]() ,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)
,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)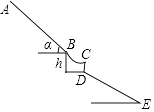
A.101.4
B.101.3
C.100.4
D.100.3
【答案】A
【解析】解:如图,作AF⊥BF于F,DG⊥EG于G. 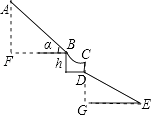
在Rt△ABF中,∵AB=90米,坡角a=40°,
∴AF=ABsin40°≈90×0.64=57.6(米).
∵陆坡DE的坡度i=1: ![]() ,
,
∴tan∠E= ![]() =
= ![]() ,
,
∴∠E=30°.
在Rt△DGE中,∵DE=85.5米,∠E=30°,
∴DG= ![]() DE=42.75米,
DE=42.75米,
∵BD之间的垂直距离h为1米,
∴该运动员在此比赛中,一共垂直下降了57.6+1+42.75=101.35≈101.4(米).
所以答案是:A.
【考点精析】根据题目的已知条件,利用关于坡度坡角问题的相关知识可以得到问题的答案,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.

练习册系列答案
相关题目