题目内容
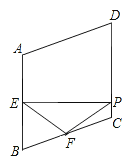
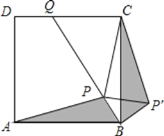
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.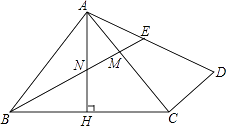
(1)若AB=3,AD= ![]() ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD= ![]() .
.
【答案】
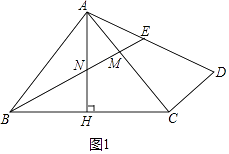
(1)解:如图1中,
在△ABM和△CAD中,
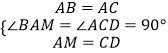 ,
,
∴△ABM≌△CAD,
∴BM=AD= ![]() ,
,
∴AM= ![]() =1,
=1,
∴CM=CA﹣AM=2,
∴S△BCM= ![]() CMBA=
CMBA= ![]() 23=3.
23=3.
(2)解:如图2中,连接EC、CN,作EQ⊥BC于Q,EP⊥BA于P.
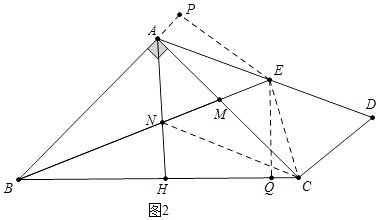
∵AE=ED,∠ACD=90°,
∴AE=CE=ED,
∴∠EAC=∠ECA,
∵△ABM≌△CAD,
∴∠ABM=∠CAD,
∴∠ABM=∠MCE,
∵∠AMB=∠EMC,
∴∠CEM=∠BAM=90°,
∵△ABM∽△ECM,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠AME=∠BMC,
,∵∠AME=∠BMC,
∴△AME∽△BMC,
∴∠AEM=∠ACB=45°,
∴∠AEC=135°,易知∠PEQ=135°,
∴∠PEQ=∠AEC,
∴∠AEQ=∠EQC,∵∠P=∠EQC=90°,
∴△EPA≌△EQC,
∴EP=EQ,∵EP⊥BP,EQ⊥BC
∴BE平分∠ABC,
∴∠NBC=∠ABN=22.5°,
∵AH垂直平分BC,
∴NB=NC,
∴∠NCB=∠NBC=22.5°,
∴∠ENC=∠NBC+∠NCB=45°,
∴△ENC的等腰直角三角形,
∴NC= ![]() EC,∴AD=2EC,
EC,∴AD=2EC,
∴2NC= ![]() AD,
AD,
∴AD= ![]() NC,
NC,
∵BN=NC,
∴AD= ![]() BN.
BN.
【解析】(1)首先根据SAS证出△ABM≌△CAD,推出BM=AD= ![]() ,然后根据勾股定理得出AM的长,再推出CM=CA﹣AM=2,从而利用∴S△BCM=
,然后根据勾股定理得出AM的长,再推出CM=CA﹣AM=2,从而利用∴S△BCM= ![]() CMBA得出答案;
CMBA得出答案;
(2)如图2中,连接EC、CN,作EQ⊥BC于Q,EP⊥BA于P,想办法证出△ENC的等腰直角三角形,即可解决问题。
【考点精析】掌握线段垂直平分线的性质和勾股定理的概念是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案