题目内容
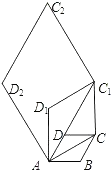
【题目】如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.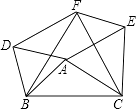
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足条件时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时,以D、A、E、F为顶点的四边形不存在.
【答案】
(1)证明:∵△ABD和△FBC都是等边三角形,
BD=BA,BF=BC,∠DBA=∠FBC=60°,
∴∠DBA﹣∠FBA=∠FBC﹣∠FBA,
∴∠DBF=∠ABC.
在△ABC和△DBF中, 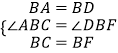
∴△ABC≌△DBF.
∴AC=DF=AE.
同理△ABC≌△EFC.
∴AB=EF=AD.
∴四边形ADFE是平行四边形.
(2)∠BAC=150°,AB=AC≠BC,∠BAC=60°
【解析】解:(2)当∠BAC=150°,∠DAE=360°﹣60°﹣60°﹣150°=90°,
∴平行四边形DAEF是矩形.
当AB=AC≠BC,有AD=AE,
∴平行四边形DAEF是菱形.
当∠BAC=60°,D、A、E、F四点共线,四边形不存在.
【考点精析】本题主要考查了等边三角形的性质和平行四边形的判定的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.

练习册系列答案
相关题目