题目内容
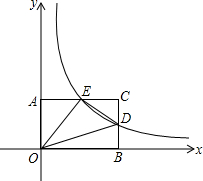
如图,在直角梯形OABC中,AB∥OC,过B点的双曲线y=
(k>0)恰好过BC的中点D,且S梯形ABCO=6,则k=______.

| k |
| x |

设B点的坐标是(m,n),点C的坐标是(p,0),则A(0,n),
∵D是BC的中点,
∴D的坐标是(
,
)
∵点D在函数y=
(k>0)的图象上,
∴k=xy=
•
=
,即(m+p)•n=4k①,
∵S梯形ABCO=6,
∴
(OC+AB)•OA=6,
×(m+p)×n=6②,
把①代入②得,
×4k=6,解得k=3.
故答案为:3.
∵D是BC的中点,
∴D的坐标是(
| m+p |
| 2 |
| n |
| 2 |
∵点D在函数y=
| k |
| x |
∴k=xy=
| m+p |
| 2 |
| n |
| 2 |
| n(m+p) |
| 4 |
∵S梯形ABCO=6,
∴
| 1 |
| 2 |
| 1 |
| 2 |
把①代入②得,
| 1 |
| 2 |
故答案为:3.

练习册系列答案
相关题目