题目内容
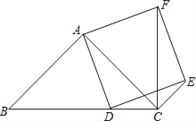
【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
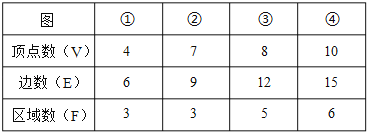
图形 | ① | ② | ③ | ④ |
顶点数(V) | ||||
边数(E) | ||||
区域数(F) |
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
【答案】(1)见表格解析;(2)V+F=E+1;(3)30.
【解析】
(1)根据图中的四个平面图形数出其顶点数、边数、区域数得出结果;
(2)根据表(1)数据总结出归律;
(3)根据题(2)的公式把20个顶点和11个区域代入即可得平面图形的边数.
(1)结和图形我们可以得出:
图①有4个顶点、6条边、这些边围成3个区域;
图②有7个顶点、9条边、这些边围成3个区域;
图③有8个顶点、12条边、这些边围成5个区域;
图④有10个顶点、15条边、这些边围成6区域.
(2)根据以上数据,顶点用V表示,边数用E表示,区域用F表示,他们的关系可表示为:V+F=E+1;
(3)把V=20,F=11代入上式得:E=V+F﹣1=20+11﹣1=30.故如果平面图形有20个顶点和11个区域,那么这个平面图形的边数为30.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目