题目内容
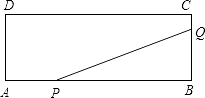
【题目】如图①,已知二次函数y=﹣x2+2x+3的图象与x轴交于点A,B,与y轴交于点C.
(1)求△ABC的面积.
(2)点M在OB边上以每秒1个单位的速度从点O向点B运动,点N在BC边上以每秒 ![]() 个单位得速度从点B向点C运动,两个点同时开始运动,同时停止.设运动的时间为t秒,试求当t为何值时,以B,M,N为顶点的三角形与△BOC相似?
个单位得速度从点B向点C运动,两个点同时开始运动,同时停止.设运动的时间为t秒,试求当t为何值时,以B,M,N为顶点的三角形与△BOC相似?
(3)如图②,点P为抛物线上的动点,点Q为对称轴上的动点,是否存在点P,Q,使得以P,Q,C,B为顶点的四边形是平行四变形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:当x=0时,y=3,即C(0,3),
当y=0时,﹣x2+2x+3=0,解得x=﹣1,x=3,即A(﹣1,0),B(3,0);
S△ABC= ![]() ABOC=
ABOC= ![]() ×[3﹣(﹣1)]×3=6
×[3﹣(﹣1)]×3=6
(2)
解:若∠BMN=90°,如图1:
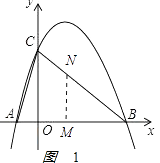 ,
,
BM=(3﹣t),BN= ![]() t,BC=
t,BC= ![]() =3
=3 ![]() ,
,
△BMN∽△BOC,
![]() =
= ![]() ,即
,即 ![]() =
= ![]() .
.
![]() t=
t= ![]() (3﹣t),解得t=
(3﹣t),解得t= ![]() ;
;
若∠BNM=90°时,如图2:
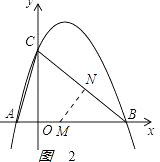 ,
,
BM=(3﹣t),BN= ![]() t,BC=
t,BC= ![]() =3
=3 ![]() ,
,
△BMN∽△BCO,
![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
3﹣t= ![]() ×
× ![]() t,解得t=1;
t,解得t=1;
综上所述:t=1或t= ![]()
(3)
解:如图3:
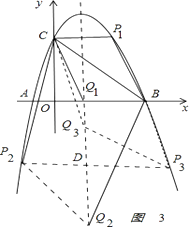 ,
,
若CB为对线,即CP∥QB,CP1=Q1B=3﹣1=2,y ![]() =yC=3,
=yC=3,
P1(2,3);
CB为边,即CB∥PQ,CB=PQ,
设P(a,b),D(1,b),Q(1,a+b﹣1).
PQ=CB,即(a﹣1)2+(1﹣a)2=18,
化简,得
a2﹣2a﹣8=0.
解得a=﹣2或a=4.
当a=﹣2时,b=﹣(﹣2)2+2×(﹣2)+3=﹣5,
即P2(﹣2,﹣5);
当a=4时,b=﹣42+2×4+3=﹣5,
即P3(4,﹣5);
综上所述:P1(2,3),P2(﹣2,﹣5),P3(4,﹣5).
【解析】(1)根据自变量与函数值的对应关系,可得A、B、C的坐标,根据三角形的面积公式,可得答案;(2)根据两角相等的两个三角形相似,可得△BMN与△BOC的关系,根据相似三角形的性质,可得关于t的方程,根据解方程,可得答案;(3)根据对边平行且相等的四边形是平行四边形,可得①BQ=PC或②BC=PQ;根据BQ∥PC,BQ=PC,可得P点坐标;根据PQ=BC,可得关于a的方程,根据解方程,可得a的值,根据自变量与函数值的对应关系,可得P点坐标.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
图形 | ① | ② | ③ | ④ |
顶点数(V) | ||||
边数(E) | ||||
区域数(F) |
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.