题目内容
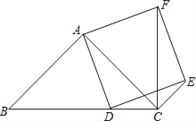
【题目】如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,连结CF,CE.
(1)求证:△ABD≌△ACF;
(2)如果BD=AC,求证:CD=CE.
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)根据正方形的性质得出![]() 求出
求出![]() 证出
证出![]() ≌
≌![]()
(2)根据△ABD≌△ACF,,推出![]() ,求出
,求出![]() 根据SAS推出△DAC≌△EFC即可.
根据SAS推出△DAC≌△EFC即可.
试题解析:证明:(1)∵四边形ADEF是正方形,
∴AD=AF,∠FAD=90°=∠BAC,
∴∠FAD-∠DAC=∠BAC-∠DAC,
∴∠FAC=∠BAD,
在△ABD和△ACF中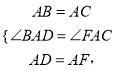
∴△ABD≌△ACF(SAS),
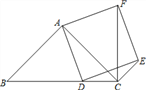
(2)∵△ABD≌△ACF,
∴BD=CF,
∵BD=AC,
∴AC=CF,
∴∠CAF=∠CFA,
∵四边形ADEF是正方形,
∴AD=EF,∠DAF=∠EFA=90°,
∴∠DAF-∠CAF=∠EFA-∠CFA,
∴∠DAC=∠EFC,
在△DAC和△EFC中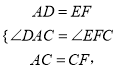
∴△DAC≌△EFC(SAS),
∴CD=CE.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
图形 | ① | ② | ③ | ④ |
顶点数(V) | ||||
边数(E) | ||||
区域数(F) |
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.