Question

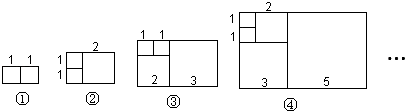
【题目】将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．
（1）如图①，对△ABC作变换[60°， ]得△AB′C′，则S△AB′C′：S△ABC=；直线BC与直线B′C′所夹的锐角为度；
（2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB′C′，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；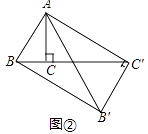
（3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．

Answer 1

【答案】
（1）3：1；60
（2）解：∵四边形 ABB′C′是矩形，

∴∠BAC′=90°．

∴θ=∠CAC′=∠BAC′﹣∠BAC=90﹣30=60°．

在 Rt△ABB′中，∠ABB'=90°，∠BAB′=60°，

∴∠AB′B=30°，

∴n= =2

（3）解：∵四边形ABB′C′是平行四边形，

∴AC′∥BB′，

又∵∠BAC=36°，

∴θ=∠CAC′=∠AC′B′=72°．

∴∠BB′A=∠BAC=36°，而∠B=∠B，

∴△ABC∽△B′BA，

∴AB：BB′=CB：AB，

∴AB2=CBBB′=CB（BC+CB′），

而 CB′=AC=AB=B′C′，BC=1，

∴AB2=1（1+AB），

∴AB= ，

∵AB＞0，

∴n= =

【解析】解：（1）根据题意得：△ABC∽△AB′C′， ∴S△AB′C′：S△ABC=（ ）2=（ ）2=3，∠B=∠B′，
∵∠ANB=∠B′NM，
∴∠BMB′=∠BAB′=60°；
所以答案是：3：1，60；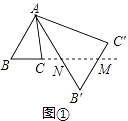

【考点精析】掌握平行四边形的性质和矩形的性质是解答本题的根本，需要知道平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；矩形的四个角都是直角，矩形的对角线相等．