题目内容
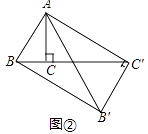
【题目】如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,那么∠B= . 
【答案】18°
【解析】解:连接DE、CE, 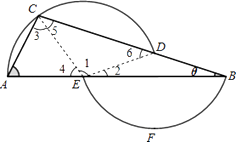
则∠2=θ,∠5=∠6=2θ,
∵∠6是△BDE的外角,
∴∠6=∠2+∠ABC=2θ,
∵∠5+∠6+∠1=180°,
∴4θ+∠1=180°①,
在△ACE中,
∵AE=CE,
∴∠3=∠CAE=63°,
∴∠4=180°﹣∠3﹣∠CAE=180°-63°-63°=54°,
∵∠4+∠1+∠2=180°,即54°+∠1+θ=180°②,
①②联立得,θ=18°.
所以答案是:18°.
【考点精析】利用圆周角定理对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目