Question

【题目】Rt△ABC中，∠C=90°，AC=8cm，BC=6cm，以点C为圆心5cm为半径的圆与直线AB的位置关系是（ ）
A.相交
B.相切
C.相离
D.无法确定

Answer 1

【答案】A
【解析】解：过C点作CD⊥AB，垂足为D， ∵∠C=90°，BC=6，AC=8，
由勾股定理，得AB= =10，
根据三角形计算面积的方法可知，BC×AC=AB×CD，
∴CD= =4.8＜5，
∴⊙C与直线AB相交．
故选A．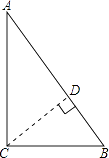

【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对直线与圆的三种位置关系的理解，了解直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点．