题目内容
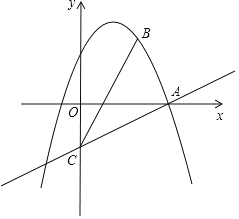
【题目】如图1,在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过
经过![]() 三点,且其对称轴为
三点,且其对称轴为![]() 其中点
其中点![]() ,点
,点![]() .
.

(1)求抛物线的解析式;
(2)①如图(1),点![]() 是直线
是直线![]() 上方抛物线上的动点,当四边形
上方抛物线上的动点,当四边形![]() 的面积取最大值时,求点
的面积取最大值时,求点![]() 的坐标;
的坐标;
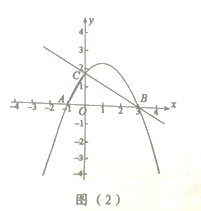
②如图(2),连接![]() 在抛物线上有一点
在抛物线上有一点![]() 满足
满足![]() ,请直接写出点
,请直接写出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ;(2)①D
;(2)①D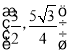 ,②
,②![]() 或
或![]()
【解析】
(1)根据点![]() ,点
,点![]() ,利用待定系数法,可得函数解析式;
,利用待定系数法,可得函数解析式;
(2)①先求出直线BC的解析式,当直线m与抛物线只有一个交点时,点D到BC的距离最远,此时△BCD取最大值,故四边形DCAB有最大值,求出b的值代入原式即可得到答案;
②根据题干条件抛物线上有一点![]() 满足
满足![]() ,通过利用待定系数法利用方程组求出直线BE的解析式,可得答案.
,通过利用待定系数法利用方程组求出直线BE的解析式,可得答案.
解:(1)由题意得:
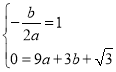
解得![]()
故抛物线的解析式是![]() .
.
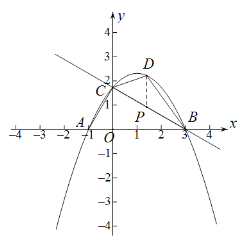
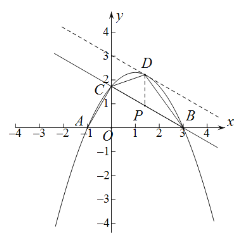
图(1) 图(2)
(2)①设直线BC的解析式为y=kx+![]() .
.
∵直线BC过点B(3,0),
∴0=3k+![]()
则k=![]() ,
,
故直线BC解析式为y=![]() x+
x+![]() .
.
设直线m解析式为![]() ,且直线m∥直线BC
,且直线m∥直线BC
当直线m与抛物线只有一个交点时,点D到BC的距离最远,此时△BCD取最大值,故四边形DCAB有最大值.
令![]() ,
,
![]()
当![]() 时
时
直线m与抛物线有唯一交点
解之得:![]()
代入原式可求得:![]()
∴D![]()
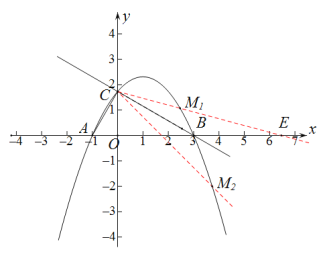
图(3)
过D作DP∥y轴交CB于点P,△DCB面积=△DPC面积+△DPB面积,
∴D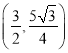
②存在,点M的横坐标为![]() 或
或![]()
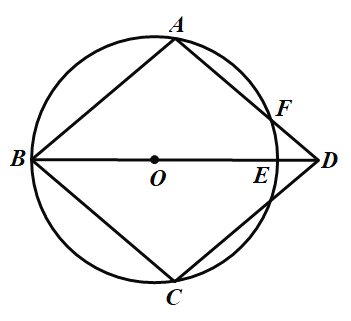
解题提示:如图3
符合条件的直线有两条: CM1和CM2(分别在CB的上方和下方)
∵在Rt△ACO中,∠ACO=30°,在Rt△COB中,∠CBO=30°,
∴∠BCM1=∠BCM2=15°
∵△BCE中,∠BCE=∠BEC2=15°
∴BC=BE=![]()
则E(![]() ,0)
,0)
设直线CE解析式为:![]()
∴![]()
解之得:k=![]()
∴直线CE解析式为:![]()
∴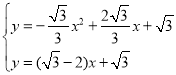
解得:x1=0,x2=2![]() -1
-1
∵ 在Rt△OCF中,∠CBO=30°,∠BCF=15°
∴在Rt△COF中, ∠CFO=45°
∴OC=OF=![]()
∴F(![]() ,0)
,0)
∴直线CF的解析式为![]()
∴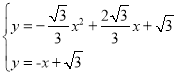
解之得:![]() (舍去),
(舍去),![]()
即点M的横坐标为:![]() 或
或![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案