题目内容
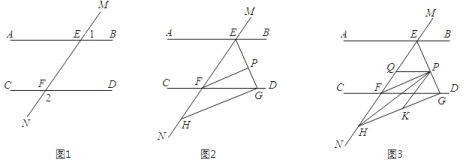
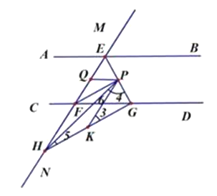
【题目】如图 1,直线 MN 与直线 AB,CD 分别交于点 E,F,∠1 与∠2 互补.
(1)试判断直线 AB 与直线 CD 的位置关系,并说明理由;
(2)如图 2,∠BEF 与∠EFD 的角平分线交于点 P,EP 与 CD 交于点 G,点 H 是 MN 上一点,且GH⊥EG,求证:PF∥GH;
(3)如图 3,在(2)的条件下,连结 PH,在 GH 上取一点 K,使得∠PKG=2∠HPK,过点 P 作 PQ 平分∠EPK 交 EF 于点 Q,问∠HPQ 的大小是否发生变化?若不变,请求出其值;若变化,说明理由.(温馨提示:三角形的三个内角和为 180°)
【答案】(1)![]() ,证明见解析 (2)证明见解析 (3)
,证明见解析 (2)证明见解析 (3)![]() 的大小不会发生变化,一直都是
的大小不会发生变化,一直都是![]()
【解析】
(1)根据邻补角的定义可得![]() 与∠2 互补,再根据同角的邻角相等,可证得
与∠2 互补,再根据同角的邻角相等,可证得![]() ,然后利用同位角相等,两直线平行,可证得结论.
,然后利用同位角相等,两直线平行,可证得结论.
(2)利用两直线平行,同旁内角互补,可得![]() ,再利用角平分线的定义去证明
,再利用角平分线的定义去证明![]() ,可得
,可得![]() ,然后根据同垂直于一条直线的两直线平行,可证得结论.
,然后根据同垂直于一条直线的两直线平行,可证得结论.
(3)利用垂直的定义可证得![]() ,利用邻补角的定义可证得
,利用邻补角的定义可证得![]() ,再由
,再由![]() ,可得
,可得![]() ,再利用角平分线的定义,可推出
,再利用角平分线的定义,可推出![]() ,由
,由![]() ,即可求出
,即可求出![]() 的度数.
的度数.
(1)∵∠1 与∠2 互补,![]() 与∠2 互补
与∠2 互补
∴![]()
∴![]() .
.
(2)∵![]()
∴![]()
∵∠BEF 与∠EFD 的角平分线交于点 P
∴![]()
∴![]() ,即
,即![]()
∵![]()
∴![]()
∴![]() .
.
(3)![]() 的大小不发生变化,理由如下
的大小不发生变化,理由如下
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵PQ平分![]()
∴![]()
∴![]()
∴![]() 的大小不会发生变化,一直都是
的大小不会发生变化,一直都是![]() .
.

练习册系列答案
相关题目