Question

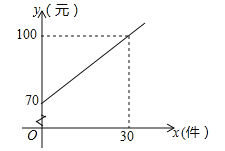
【题目】某商场经销一种商品，已知其每件进价为40元。现在每件售价为70元，每星期可卖出500件。该商场通过市场调查发现：若每件涨价1元，则每星期少卖出10件；若每件降价1元，则每星期多卖出m（m为正整数）件。设调查价格后每星期的销售利润为W元。

（1）设该商品每件涨价x（x为正整数）元，

①若x＝5，则每星期可卖出____件，每星期的销售利润为_____元；

②当x为何值时，W最大，W的最大值是多少。

（2）设该商品每件降价y（y为正整数）元，

①写出W与Y的函数关系式，并通过计算判断：当m＝10时每星期销售利润能否达到（1）中W的最大值；

②若使y＝10时，每星期的销售利润W最大，直接写出W的最大值为_____。

（3）若每件降价5元时的每星期销售利润，不低于每件涨价15元时的每星期销售利润，求m的取值范围。

Answer 1

【答案】(1)①450,15750;②x=10,最大值为16000;(2)①不能，理由见解析； ②20000元；（3）m≥26

【解析】试题分析：①直接进行计算即可.

②根据利润=每件的利润销售量即可写出函数关系式，进而求得利润的最大值.

①根据利润=每件的利润销售量写出与的关系式，根据二次函数的性质求出最大值和中的最大值进行比较即可.

②直接写出最大利润即可.

根据题意，列出不等式，解不等式即可.

试题解析：（1）①当时，每星期可卖出：件，

每星期的销售利润为：元.

故答案为：

②根据题意得：

W＝,

∵W是x的二次函数，且－10＜0，

∴当时，W最大,

W最大值＝,

答：当x＝10时，W最大，最大值为16000.

（2）①W＝（70－40－y）（500＋my）,

W＝,

当m＝10时，W＝,

∵W是y的二次函数，且－10＜0，

∴当y＝时，W最大，当y＞－10时，W随y的增大而减小，

∵y为正整数，

∴当y=1时，W最大，W最大=－10－200＋15000=14790,

14790＜16000

答：销售利润不能达到（1）中W的最大值，

②当时，即 解得：

此时，元.

故答案为：20000元.

（3）降价5元时销售利润为：W＝（70－40－5）（500＋5m）=125m＋125000,

涨价15元时的销售利润为：W=＋3000＋15000=15750,

根据题意，得125m＋12500≥15750,

解得:m≥26,

答：m的取值范围是m≥26.