题目内容
【题目】如图，D、B、C三点在同一条直线上，∠C=50°，∠FBC=80°．问：∠DBF的平分线BE与AC有怎样的位置关系？并说明理由．
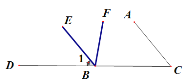
解：BE与AC一定平行．
∵D、B、C三点在同一条直线上，
∴∠DBF+∠FBC=180°（ ）．
又∵∠FBC=80°（已知）．
∴∠DBF= ．
又∵BE平分∠DBF（已知）．
∴
（ ）．
又∵∠C=50°（已知），
∴∠ =∠ （ ），
∴ ∥ ．（ ）
【答案】BE与AC一定平行，理由见解析
【解析】
首先由平角定义得出∠DBF，然后根据角平分线的性质，得出∠1=∠C，再根据同位角相等，两直线平行即可判定.
BE与AC一定平行；
∵D、B、C三点在同一条直线上，
∴∠DBF+∠FBC=180°（平角定义）．
又∵∠FBC=80°（已知）．
∴∠DBF=100°．
又∵BE平分∠DBF（已知）．
∴
（等式性质）．
又∵∠C=50°（已知），
∴∠1=∠C（等式性质），
∴EB∥AC．（同位角相等，两直线平行）
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
