Question

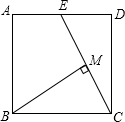
ABCD是边长为1的正方形，△BPC是等边三角形，则△BPD的面积为（　　）

A． 1 4

B． 3 -1 4

C． 1 8

D． 2 3 -1 8

Answer 1

△BPD的面积等于△BCP和△CDP面积和减去△BCD的面积
因此本题求解△BCP、△CDP面积和△BCD的面积即可，
S_△BCP=

1

2

×1×

3

2

=

3

4

，
S_△CDP=

1

2

×1×

1

2

=

1

4

，
S_△BCD=

1

2

×1×1=

1

2

，
∴S_△BPD=

3

4

+

1

4

-

1

2

=

3 -1

4

．
故选B．