题目内容
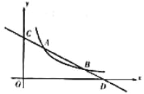
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点
)的图像分别交于点![]() 和点
和点![]() ,与坐标轴分别交于点
,与坐标轴分别交于点![]() 和点
和点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)若点![]() 是
是![]() 轴上一动点,当
轴上一动点,当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)(2,0)或(
;(2)(2,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)首先确定A、B两点坐标,再利用待定系数法即可解决问题;
(2)分两种情形讨论求解即可.
试题解析:(1)∵y=kx+b与反比例函数![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),
(x>0)的图象分别交于点 A(m,3)和点B(6,n),
∴m=2,n=1,∴A(2,3),B(6,1),
则有![]() ,解得
,解得 ,
,
∴直线AB的解析式为![]()
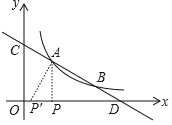
(2)如图①当PA⊥OD时,∵PA∥CC,
∴△ADP∽△CDO,此时p(2,0).
②当AP′⊥CD时,易知△P′DA∽△CDO,
∵直线AB的解析式为![]() ,
,
∴直线P′A的解析式为y=2x﹣1,
令y=0,解得x=![]() ,∴P′(
,∴P′(![]() ,0),
,0),
综上所述,满足条件的点P坐标为(2,0)或(![]() ,0).
,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

