��Ŀ����
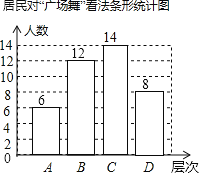
����Ŀ���������ڵġ��㳡�衱����ý���ע��С�����˽ⱾС������ԡ��㳡�衱�Ŀ���������һ�η��ĸ���εij������飨�ĸ����Ϊ��A���dz���ͬ��B����ͬ��Ҫ��ʱ�����ƣ�C������ν��D������ͬ�������ѵ��������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�еı�Ϣ����������⣺

��1�����α����ľ����������� ���ˣ�������ͳ��ͼ����������
��2��ͼ�С����Ķ������� ���ȣ���С����3000����������ƶԡ��㳡�衱��ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ����
��3�����˽⣬�ס��ҡ���������λ����Ͷ����ͬƱ��С���������λ���������ѡ����λ�˽��������������б�����״ͼ�ķ������ǡ��ѡ�м��ҵĸ��ʣ�
���𰸡���1��40������������2��54���ԡ��㳡�衱��ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ��1350�ˣ���3����������![]() ��
��
��������
��1����A��ε�������������ռ�İٷֱȵõ���������������ټ����C��ε�������Ȼ��ȫ����ͳ��ͼ��
��2����A��ε�������ռ�İٷֱȳ���360��õ������Ķ�������3000�ֱ����������A��B��ε�������ռ�İٷֱȣ������ǵĺͿɹ��Ƴ�С���ԡ��㳡�衱��ʾ��ͬ������A��κ�B��Σ���������
��3������״ͼչʾ����12�ֵȿ��ܵĽ�������ҳ�ǡ��ѡ�м��ҵĽ������Ȼ����ݸ��ʹ�ʽ��⣮
�⣺��1��12��30%��40��
���Ա��α����ľ���������40�ˣ�
C��ε�����Ϊ40��6��12��8��14���ˣ���
����ͳ��ͼ����Ϊ��
��2��������360���![]() ��54�㣬
��54�㣬
3000��![]() ��1350��
��1350��
���Թ��ƶԡ��㳡�衱��ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ��1350�ˣ�
�ʴ�Ϊ40��54��
��3������״ͼΪ��

����12�ֵȿ��ܵĽ����������ǡ��ѡ�м��ҵĽ����Ϊ2��
����ǡ��ѡ�м��ҵĸ��ʣ�![]() ��
��![]() ��
��