��Ŀ����
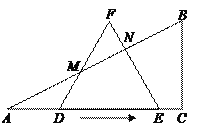
����Ŀ����ͼ����֪Rt��ABC�У���A��30�㣬AC��6���߳�Ϊ4�ĵȱߡ�DEF������AC�˶���A��D��E��C�ĵ㹲�ߣ�.���ȱߡ�DEF�ı�DF��EF��Rt��ABC�ı�AB�ֱ��ཻ�ڵ�M��N��M��N����A��B�غϣ�ʱ��
��AD=x��
��1�����FMN����״�� _______ ,��ADM����״�� _______��
��2����ABC���DEF�ص����ֵ����Ϊy����y����x�ĺ�������ʽ����д����ȡֵ��Χ��
��3�����Ե�MΪԲ�ģ�MNΪ�뾶��Բ���AC��EFͬʱ���У����ʱMN�ij���
���𰸡���1��ֱ�������� ��������������2��![]() ����3��
����3��![]()
��������
��1��ֱ�������Ρ�����������
��2���ߡ�AD���ǵ��������Σ�
��DM=AD=x �� FM=4-x.
�֡ߡ�FED=60�㣬��A=30�㣬 ���FNM=90��
��MN=MF��SinF=![]() ��FN=
��FN=![]() MF=
MF=![]() ��4-x��
��4-x��![]()
��0<x��2ʱ��![]()
��2��x<4ʱ�� CE=AE�DAC=4+x-6=x-2
�ߡ�BCE=90�㣬��PEA=60�㣬
��PC=![]()
��![]()
�� =S��DEF�DS��FMN�DS��PCE=![]()
��3������M��MG��AC�ڵ�G���ɣ�2����DM=x
�ߡ�MDG=60�㣬 ��MG=![]()
����MNF=90�㣬��MFN=60�㣬��MN=![]()
Ҫʹ�Ե�MΪԲ�ģ�MN��Ϊ�뾶��Բ���AC��EF���У�����MG=MN��
����![]() ���x=2��
���x=2��
Բ�İ뾶MN=![]()