Question

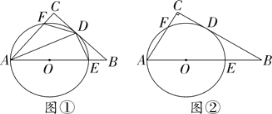
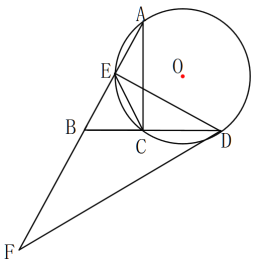
【题目】已知菱形 ABCD 中， ADC 120 ， F 为 DB 延长线上一点， E 为 DA 延长线上一点， 且 BF DE ， 连 CF 、 EF ， 点 O 为 BD 的中点， 过 O 作 OM AB 交 EF 于 M ， 若OM ，AE 1，则 AB 的长度为（ ）

A.B.2C.D.

Answer 1

【答案】C

【解析】

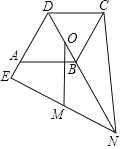
连接CM，CO，CE，判定△EDC≌△NBC，即可得到∠DCE=∠BCN，EC=NC，进而得出△ECN为等边三角形，依据∠CMO=∠CED，∠CDE=∠COM=120°，可得△CDE∽△COM，再根据相似三角形的性质，即可得到AD，AB的长．

解：如图，连接CM，CO，CE，

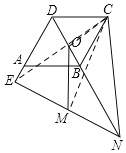
∵菱形ABCD中，∠ADC=120°，N为DB延长线上一点，
∴∠ADC=∠NBC=120°，CD=CB，而DE=BN，
∴△EDC≌△NBC（SAS），
∴∠DCE=∠BCN，EC=NC，
又∵∠DCE+∠ECB=60°，
∴∠BCN+∠ECB=60°，
∴∠ECN=60°，
∴△ECN为等边三角形，
∴∠CNM=60°，
∴∠CNM+∠COM=180°，
∴M，N，O，C四点共圆，
∴∠CNB=∠CMO，
又∵∠CNB=∠CED，
∴∠CMO=∠CED，
又∵∠CDE=∠COM=120°，
∴△CDE∽△COM，

，即

解得

又∵AE=1，

故选：C