ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§![]() ΒΡΕΞΒψΉχ±ξΖ÷±πΈΣ
ΒΡΕΞΒψΉχ±ξΖ÷±πΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() .Ε·Βψ
.Ε·Βψ![]() Θ§
Θ§![]() Ά§ ±¥”Βψ
Ά§ ±¥”Βψ![]() ≥ωΖΔΘ§
≥ωΖΔΘ§![]() ―Ί
―Ί![]() Θ§
Θ§![]() ―Ί’έœΏ
―Ί’έœΏ![]() Θ§Ψυ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»“ΤΕ·Θ§Β±“ΜΗωΕ·ΒψΒΫ¥ο÷’Βψ
Θ§Ψυ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»“ΤΕ·Θ§Β±“ΜΗωΕ·ΒψΒΫ¥ο÷’Βψ![]() ±Θ§Νμ“ΜΗωΕ·Βψ“≤Υφ÷°ΆΘ÷Ι“ΤΕ·Θ§“ΤΕ· ±ΦδΦ«ΈΣ
±Θ§Νμ“ΜΗωΕ·Βψ“≤Υφ÷°ΆΘ÷Ι“ΤΕ·Θ§“ΤΕ· ±ΦδΦ«ΈΣ![]() ΟκΘ§Ν§Ϋ”
ΟκΘ§Ν§Ϋ”![]() .
.
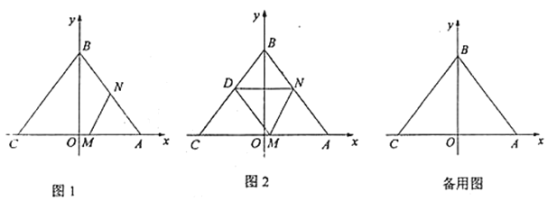
Θ®ΔώΘ©»γΆΦ1Θ§Β±Βψ![]() “ΤΕ·ΒΫ
“ΤΕ·ΒΫ![]() ÷–Βψ ±Θ§«σ¥Υ ±
÷–Βψ ±Θ§«σ¥Υ ±![]() ΒΡ÷ΒΦΑ
ΒΡ÷ΒΦΑ![]() ΒψΉχ±ξΘΜ
ΒψΉχ±ξΘΜ
Θ®ΔρΘ©‘Ύ“ΤΕ·Ιΐ≥Χ÷–Θ§ΫΪ![]() ―Ί÷±œΏ
―Ί÷±œΏ![]() Ζ≠’έΘ§Βψ
Ζ≠’έΘ§Βψ![]() ΒΡΕ‘≥ΤΒψΈΣ
ΒΡΕ‘≥ΤΒψΈΣ![]() .
.
ΔΌ»γΆΦ2Θ§Β±Βψ![]() «ΓΚΟ¬δ‘Ύ
«ΓΚΟ¬δ‘Ύ![]() ±Ώ…œΒΡΒψ
±Ώ…œΒΡΒψ![]() ¥Π ±Θ§«σ¥Υ ±
¥Π ±Θ§«σ¥Υ ±![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
ΔΎΒ±Βψ![]() “ΤΕ·ΒΫΒψ
“ΤΕ·ΒΫΒψ![]() ±Θ§Βψ
±Θ§Βψ![]() ¬δ‘ΎΒψ
¬δ‘ΎΒψ![]() ¥ΠΘ§«σ¥Υ ±Βψ
¥ΠΘ§«σ¥Υ ±Βψ![]() ΒΡΉχ±ξΘ®÷±Ϋ”–¥≥ωΫαΙϊΦ¥Ω…Θ©.
ΒΡΉχ±ξΘ®÷±Ϋ”–¥≥ωΫαΙϊΦ¥Ω…Θ©.
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©![]() ,Βψ
,Βψ![]() Ήχ±ξΈΣ
Ήχ±ξΈΣ![]() ; Θ®ΔρΘ©ΔΌ
; Θ®ΔρΘ©ΔΌ![]() ; ΔΎ
; ΔΎ![]() ΒψΉχ±ξΈΣ
ΒψΉχ±ξΈΣ![]()
ΓΨΫβΈωΓΩ
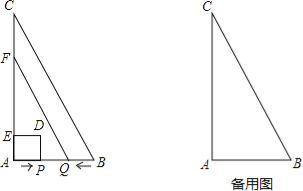
(1)ΗυΨίΒψΒΡΉχ±ξΘ§“‘«σΒΟABΒΡ≥ΛΘ§”…”ΎN «ABΒΡ÷–ΒψΘ§Ω…ΒΟANΒΡ≥ΛΕ»Θ§¥”Εχ«σ≥ωtΘ§Φ¥Ω…«σMΒψΚζΉχ±ξ;
(2)ΔΌ”…Ζ≠Ή≈ΒΡ–‘÷ Ω…ΒΟΥΡ±Ώ–Έ![]() ΈΣΝβ–ΈΘ§‘ρ”–
ΈΣΝβ–ΈΘ§‘ρ”–![]() ÷αΘ§Ω…ΒΟΒΫ
÷αΘ§Ω…ΒΟΒΫ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§¥”Εχ«σ≥ωt.
Θ§¥”Εχ«σ≥ωt.
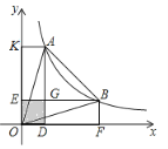
ΔΎΗυΨίœύΥΤΩ…“‘«σ≥ωN(![]() )Θ§…ηE(x,y),ΗυΨίΙ¥Ι…Ε®άμΝ–≥ωΖΫ≥ΧΉι:EM=6,EN=5,ΫβΒΟΦ¥Ω…«σ≥ωΒψE.
)Θ§…ηE(x,y),ΗυΨίΙ¥Ι…Ε®άμΝ–≥ωΖΫ≥ΧΉι:EM=6,EN=5,ΫβΒΟΦ¥Ω…«σ≥ωΒψE.
Θ®ΔώΘ©ΓΏ![]() Θ§
Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() Θ§Γύ
Θ§Γύ![]() .
.
Β±Βψ![]() “ΤΕ·ΒΫ
“ΤΕ·ΒΫ![]() ÷–Βψ ±Θ§”…Χβ“βΩ…ΒΟ
÷–Βψ ±Θ§”…Χβ“βΩ…ΒΟ![]() Θ§
Θ§
Γύ![]() .
.
ΓΏ![]() Θ§
Θ§
ΓύΒψ![]() Ήχ±ξΈΣ
Ήχ±ξΈΣ![]() .
.
Θ®ΔρΘ©ΔΌ”…Χβ“βΩ…ΒΟ![]() Θ§
Θ§
ΓΏ![]() ―Ί÷±œΏ
―Ί÷±œΏ![]() Ζ≠’έΘ§Βψ
Ζ≠’έΘ§Βψ![]() ¬δ‘ΎΒψ
¬δ‘ΎΒψ![]() ¥ΠΘ§
¥ΠΘ§
Γύ![]() Θ§
Θ§
ΓύΥΡ±Ώ–Έ![]() ΈΣΝβ–ΈΘ§
ΈΣΝβ–ΈΘ§
Γύ![]() Θ§
Θ§![]() ÷αΘ§
÷αΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() Θ§
Θ§
ΫβΒΟ![]() .
.
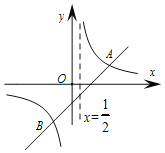
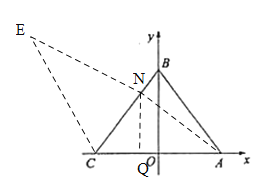
Θ®ΔρΘ©ΔΎΙΐNΉωX÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣQΘ§”…ΓςCNQΓΉΓςBCOΘ§
”÷ΓΏBN=1,AC=6,BC=5,
Γύ![]() ,ΓύN(
,ΓύN(![]() )Θ§
)Θ§
…ηE(x,y),«“CE=6,EN=5,
‘ρ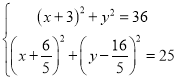
ΫβΒΟΘΚ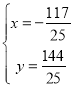
![]() ΒψΉχ±ξΈΣ
ΒψΉχ±ξΈΣ![]() .
.

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ