题目内容
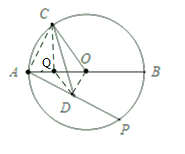
【题目】如图,AB是![]() O的直径,AB=4,C为
O的直径,AB=4,C为![]() 的三等分点(更靠近A点),点P是
的三等分点(更靠近A点),点P是![]() O上一个动点,取弦AP的中点D,则线段CD的最大值为( )
O上一个动点,取弦AP的中点D,则线段CD的最大值为( )

A.2B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
取OA的中点Q,连接DQ,OD,CQ,根据条件可求得CQ长,再由垂径定理得出OD⊥AP,由直角三角形斜边中线等于斜边一半求得QD长,根据当C,Q,D三点共线时,CD长最大求解.
解:如图,取AO的中点Q,连接CQ,QD,OD,
∵C为![]() 的三等分点,
的三等分点,
∴![]() 的度数为60°,
的度数为60°,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∵Q为OA的中点,
∴CQ⊥OA,∠OCQ=30°,
∴OQ=![]() ,
,
由勾股定理可得,CQ=![]() ,
,
∵D为AP的中点,
∴OD⊥AP,
∵Q为OA的中点,
∴DQ=![]() ,
,
∴当D点CQ的延长线上时,即点C,Q,D三点共线时,CD长最大,最大值为![]() .
.
故选D

练习册系列答案
相关题目