题目内容
【题目】如图,在![]() 中,AD是BC边上的高,
中,AD是BC边上的高,![]() 。
。
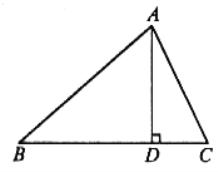
(1)求证:AC=BD
(2)若![]() ,求AD的长。
,求AD的长。
【答案】(1)证明见解析;(2)8
【解析】
(1)由于tanB=cos∠DAC,所以根据正切和余弦的概念证明AC=BD;
(2)设AD=12k,AC=13k,然后利用题目已知条件即可解直角三角形.
(1)证明:∵AD是BC上的高,
∴AD⊥BC,
∴∠ADB=90°,∠ADC=90°,
在Rt△ABD和Rt△ADC中,
∵tanB=![]() ,cos∠DAC=
,cos∠DAC=![]() ,
,
又∵tanB=cos∠DAC,
∴![]() =
=![]() ,
,
∴AC=BD;
(2)在Rt△ADC中,sinC=![]() ,
,
故可设AD=12k,AC=13k,
∴CD=![]() =5k,
=5k,
∵BC=BD+CD,又AC=BD,
∴BC=13k+5k=18k,
由已知BC=12,
∴18k=12,
∴k=![]() ,
,
∴AD=12k=12×![]() =8.
=8.

练习册系列答案
相关题目