题目内容
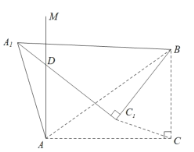
【题目】如图,在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一定角度后得到
顺时针旋转一定角度后得到![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 的长为__________.
的长为__________.
【答案】![]()
【解析】
利用折叠的性质可证得△ABC≌△A1BC1 , 由此可以推出AB=A1B,BC=B1C,∠ABC=∠A1BC1 , 再证明∠A1BA=∠C1BC,利用有两组角对应相等的两三角形相似,可证△A1BA∽△C1BC,利用相似三角形的对应边成比例,可得到AB与BC之间的数量关系,利用锐角三角函数的定义及勾股定理,可以求出AB,BC的长,过C1作C1Q⊥BC交BC,AN于点Q,点P,设PC1=x,CQ=y,可建立关于x,y的方程组,解方程组求出x,y的值,即可求出AD的长.
根据题意,可得△ABC≌△A1BC1 ,
∴AB=A1B,BC=B1C,∠ABC=∠A1BC1,
∵∠ABC=∠A1BA+∠ABC1 , ∠A1BC1=∠C1BC+∠ABC1,
∴∠A1BA=∠C1BC,
∴△A1BA∽△C1BC,
∵CC1= ![]() AA1,
AA1,
∴AB= ![]() BC,
BC,
∴sin∠BAC=sin∠BA1D= ![]() ,
,
在Rt△ABC中,设AB=5x,BC=3x,
AB2=AC2+BC2 , 即(5x)2=162+(3x)2,
解方程(5x)2=162+(3x)2 , 得x1=4,x2=-4(舍),
∴BC=BC1=DC1=12, AC=A1C1=16,
过C1作C1Q⊥BC交BC,AN于点Q,点P,
设PC1=x,CQ=y,![]() ,
,
解得: 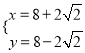 或
或 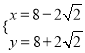 ,
,
∴AD=12+4 ![]() 或12-4
或12-4 ![]() ,
,
∵AD<BC,
∴AD=12-4 ![]() .
.

【题目】已知二次函数y=﹣2x2﹣4x+6.
(1)用配方法求出函数的顶点坐标;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
表1:四种款式电脑的利润
电脑款式 | A | B | C | D |
利润(元/台) | 160 | 200 | 240 | 320 |
表2:甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量(台) | 20 | 15 | 10 | 5 |
乙店销售数量(台)8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识,解决下列问题:
(1)从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为 ;
(2)经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()