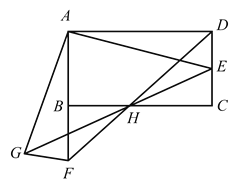
ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżÄłÊßČËŒÓč€č«ËŸÏÈșóÁœĆúŽÎÊŐčșŃóŽĐčČ100¶ÖŁź”ÚÒ»ĆúŃóŽĐŒÛžńÎȘ4000ÔȘ/¶ÖŁ»ÒòŃóŽĐŽóÁżÉÏÊĐŁŹ”Ú¶țĆúŒÛžń”űÖÁ1000ÔȘ/¶ÖŁźŐâÁœĆúŃóŽĐčČÓĂÈ„16ÍòÔȘŁź
(1)ÇóÁœĆúŽÎčșœűŃóŽĐžś¶àÉÙ¶ÖŁ»
(2)č«ËŸÊŐčșșó¶ÔŃóŽĐœűĐĐŒÓ耣Ź·ÖÎȘŽÖŒÓč€șÍŸ«ŒÓč€ÁœÖÖŁșŽÖŒÓč€Ăż¶ÖÀûÈó400ÔȘŁŹŸ«ŒÓč€Ăż¶ÖÀûÈó1000ÔȘŁźÒȘÇóŸ«ŒÓč€ÊęÁżČ»¶àÓÚŽÖŒÓč€ÊęÁż”ÄÈ걶ŁźÎȘ»ń”ĂŚîŽóÀûÈóŁŹŸ«ŒÓč€ÊęÁżÓŠÎȘ¶àÉÙ¶ÖŁżŚîŽóÀûÈóÊǶàÉÙŁż
ĄŸŽđ°žĄżŁš1Ł©”ÚÒ»ĆúčșœűŃóŽĐ20¶ÖŁŹ”Ú¶țĆúčșœűŃóŽĐ80¶ÖŁ»Łš2Ł©Ÿ«ŒÓč€ÊęÁżÓŠÎȘ75¶ÖŁŹŚîŽóÀûÈóÊÇ85000ÔȘ
ĄŸœâÎöĄż
Łš1Ł©Éè”ÚÒ»ĆúčșœűŃóŽĐx¶ÖŁŹ”Ú¶țĆúčșœűŃóŽĐy¶ÖŁŹččœš·œłÌŚéŒŽżÉœâŸöÎÊÌ⣻
Łš2Ł©É蟫ŒÓč€m¶ÖŁŹŚÜÀûÈóÎȘwÔȘŁŹÔòŽÖŒÓč€(100-m)¶ÖŁŹÓÉŸ«ŒÓč€ÊęÁżČ»¶àÓÚŽÖŒÓč€ÊęÁż”ÄÈ걶Çółöm”ÄÈĄÖ”·¶Î§ŁŹžùŸĘŚÜÀûÈów=Ÿ«ŒÓ耔ÄÀûÈó+ŽÖŒÓ耔ÄÀûÈóÁĐłöșŻÊęœâÎöÊœŁŹÀûÓĂÒ»ŽÎșŻÊę”ÄĐÔÖÊŒŽżÉœâŸöÎÊÌ⣟
œâŁșŁš1Ł©Éè”ÚÒ»ĆúčșœűŃóŽĐx¶ÖŁŹ”Ú¶țĆúčșœűŃóŽĐy¶ÖŁź
ÓÉÌâÒâ
![]() ŁŹ
ŁŹ
œâ”Ă
![]() ŁŹ
ŁŹ
ŽđŁș”ÚÒ»ĆúčșœűŃóŽĐ20¶ÖŁŹ”Ú¶țĆúčșœűŃóŽĐ80¶ÖŁź
Łš2Ł©É蟫ŒÓč€m¶ÖŁŹŚÜÀûÈóÎȘwÔȘŁŹÔòŽÖŒÓč€(100-m)¶ÖŁź
ÓÉmĄÜ3(100-m)ŁŹ
œâ”ĂmĄÜ75ŁŹ
ÀûÈów=1000m+400(100-m)=600m+40000ŁŹ
Ąß600ŁŸ0ŁŹ
ĄàwËæm”ÄÔöŽó¶űÔöŽóŁŹ
Ąàm=75ʱŁŹwÓĐŚîŽóÖ”ÎȘ85000ÔȘŁź
ŽđŁșŸ«ŒÓč€ÊęÁżÓŠÎȘ75¶ÖŁŹŚîŽóÀûÈóÊÇ85000ÔȘŁź

ĄŸÌâÄżĄż”çÆśŚšÓȘ”ê”ÄŸÓȘÀûÈóÊÜ”ŰÀíλÖĂĄąčËżÍÏû·ŃÄÜÁŠ”ÈÒòËŰ”ÄÓ°ÏìŁŹÄłÆ·ĆÆ”çÄÔŚšÓȘ”êÉèÓĐŒŚĄąÒÒÁœŒÒ·Ö”êŁŹŸùÏúÊÛAĄąBĄąCĄąDËÄÖÖżîÊœ”Ä”çÄÔŁŹĂżÖÖżîÊœ”çÄÔ”ÄÀûÈóÈç±í1ËùÊŸŁźÏÖŽÓŒŚĄąÒÒÁœ”êĂżÔÂÊÛłö”Ä”çÄÔÖĐžśËæ»úłéÈĄËùŒÇÂŒ”Ä50Ìš”çÄԔĿîÊœŁŹÍłŒÆžśÖÖżîÊœ”çÄÔ”ÄÏúÊÛÊęÁżŁŹÈç±í2ËùÊŸŁź
±í1ŁșËÄÖÖżîÊœ”çÄÔ”ÄÀûÈó
”çÄÔżîÊœ | A | B | C | D |
ÀûÈóŁšÔȘ/ÌšŁ© | 160 | 200 | 240 | 320 |
±í2ŁșŒŚĄąÒÒÁœ”ê”çÄÔÏúÊÛÇéżö
”çÄÔżîÊœ | A | B | C | D |
ŒŚ”êÏúÊÛÊęÁżŁšÌšŁ© | 20 | 15 | 10 | 5 |
ÒÒ”êÏúÊÛÊęÁżŁšÌšŁ©8 | 8 | 10 | 14 | 18 |
ÊÔÔËÓĂÍłŒÆÓëžĆÂÊÖȘʶŁŹœâŸöÏÂÁĐÎÊÌâŁș
Łš1Ł©ŽÓŒŚ”êĂżÔÂÊÛłö”Ä”çÄÔÖĐËæ»úłéÈĄÒ»ÌšŁŹÆäÀûÈóČ»ÉÙÓÚ240ÔȘ”ÄžĆÂÊÎȘĄĄ ĄĄŁ»
Łš2Ł©ŸÊĐłĄ”śČé·ąÏÖŁŹŒŚĄąÒÒÁœ”êĂżÔ”çÄԔČÜÏúÁżÏà”±ŁźÏÖÓÉÓÚŚÊœđÏȚÖÆŁŹĐè¶ÔÆäÖĐÒ»ŒÒ·Ö”êŚśłöÔĘÍŁÓȘÒ””ÄŸö¶šŁŹÈôŽÓĂżÌš”çÄÔ”ÄÆœŸùÀûÈó”ÄœÇ¶ÈżŒÂÇŁŹÄăÈÏÎȘÓŠ¶ÔÄÄŒÒ·Ö”êŚśłöÔĘÍŁÓȘÒ””ÄŸö¶šŁżČąË”ĂśÀíÓÉŁź