题目内容
如图,在平面直角坐标系中,已知抛物线y=-
x2+bx+c经过点A(0,1)、B(3,
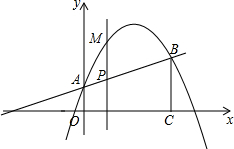
)两点,BC⊥x轴,垂足为C.点P是线段AB上的一动点(不与A,B重合),过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
(1)求此抛物线的函数表达式;
(2)连结AM、BM,设△AMB的面积为S,求S关于t的函数关系式,并求出S的最大值;
(3)连结PC,当t为何值时,四边形PMBC是菱形?
| 5 |
| 4 |
| 5 |
| 2 |
(1)求此抛物线的函数表达式;
(2)连结AM、BM,设△AMB的面积为S,求S关于t的函数关系式,并求出S的最大值;
(3)连结PC,当t为何值时,四边形PMBC是菱形?

(1)∵抛物线y=-
x2+bx+c经过点A(0,1)、B(3,
)两点,
∴
,
解得:
,
∴抛物线解析式为:y=-
x2+
x+1;
(2)∵设点P的横坐标为t,
∴M点坐标为:(t,-
t2+
t+1),
设直线AB的解析式为:y=kx+b,
则
,
解得:
,
∴直线AB的解析式为:y=
x+1,
∵P点在直线AB上,点P的横坐标为t,
∴P点的纵坐标为:
t+1,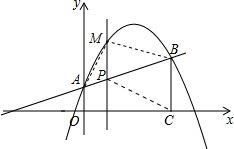
∴MP=-
t2+
t+1-
t-1=-
t2+
t,
∴S△AMB=S△AMP+S△BMP=
×(-
t2+
t)×t+
×(-
t2+
t)×(3-t)
=-
t2+
t,
当t=
时,S最大值=
;
(3)t=1时,四边形PMBC为菱形.
理由:∵BC∥PM,当BC=MP时,四边形MPCB是平行四边形,
当BC=PC时,平行四边形PMBC是菱形,
∵B(3,
),
∴BC=
,即MP=PC=
=-
t2+
t,
解得:t1=1,t2=2,
PC=
=
,
解得:t1=1,t2=3,
只有同时满足两个方程才可以,
故t=1.此时四边形PMBC为菱形.
| 5 |
| 4 |
| 5 |
| 2 |
∴
|
解得:
|
∴抛物线解析式为:y=-
| 5 |
| 4 |
| 17 |
| 4 |
(2)∵设点P的横坐标为t,
∴M点坐标为:(t,-
| 5 |
| 4 |
| 17 |
| 4 |
设直线AB的解析式为:y=kx+b,
则
|
解得:
|
∴直线AB的解析式为:y=
| 1 |
| 2 |
∵P点在直线AB上,点P的横坐标为t,
∴P点的纵坐标为:
| 1 |
| 2 |

∴MP=-
| 5 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
∴S△AMB=S△AMP+S△BMP=
| 1 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
=-
| 15 |
| 8 |
| 45 |
| 8 |
当t=
| 3 |
| 2 |
| 135 |
| 32 |
(3)t=1时,四边形PMBC为菱形.
理由:∵BC∥PM,当BC=MP时,四边形MPCB是平行四边形,
当BC=PC时,平行四边形PMBC是菱形,
∵B(3,
| 5 |
| 2 |
∴BC=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 15 |
| 4 |
解得:t1=1,t2=2,
PC=
(
|
| 5 |
| 2 |
解得:t1=1,t2=3,
只有同时满足两个方程才可以,
故t=1.此时四边形PMBC为菱形.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目

 的图象上一个动点,点P的横坐标是m,且m>3,过点P作PM,PM交直线AB于M.
的图象上一个动点,点P的横坐标是m,且m>3,过点P作PM,PM交直线AB于M.
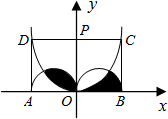

 距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,
距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,