题目内容
已知:在平面直角坐标系中,抛物线y=-
x2+bx+3交x轴于A、B两点,交y轴于点C,且对称轴为x=-2,点P(0,t)是y轴上的一个动点.

(1)求抛物线的解析式及顶点D的坐标.
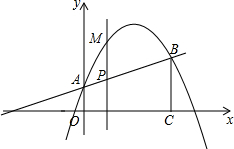
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
| 1 |
| 4 |

(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
(1)对称轴为x=-
=-2,
解得b=-1,
所以,抛物线的解析式为y=-
x2-x+3,
∵y=-
x2-x+3=-
(x+2)2+4,
∴顶点D的坐标为(-2,4);
(2)令y=0,则-
x2-x+3=0,
整理得,x2+4x-12=0,
解得x1=-6,x2=2,
∴点A(-6,0),B(2,0),
如图1,过点D作DE⊥y轴于E,
∵0≤t≤4,
∴△PAD的面积为S=S梯形AOED-S△AOP-S△PDE,
=
×(2+6)×4-
×6t-
×2×(4-t),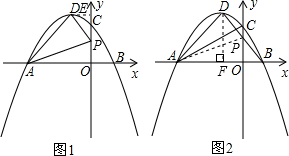
=-2t+12,
∵k=-2<0,
∴S随t的增大而减小,
∴t=4时,S有最小值,最小值为-2×4+12=4;
(3)如图2,过点D作DF⊥x轴于F,
∵A(-6,0),D(-2,4),
∴AF=-2-(-6)=4,
∴AF=DF,
∴△ADF是等腰直角三角形,
∴∠ADF=45°,
由二次函数对称性,∠BDF=∠ADF=45°,
∴∠PDA=90°时点P为BD与y轴的交点,
∵OF=OB=2,
∴PO为△BDF的中位线,
∴OP=
DF=2,
∴点P的坐标为(0,2),
由勾股定理得,DP=
=2
,
AD=
AF=4
,
∴
=
=2,
令x=0,则y=3,
∴点C的坐标为(0,3),OC=3,
∴
=
=2,
∴
=
,
又∵∠PDA=90°,∠COA=90°,
∴Rt△ADP∽Rt△AOC.
| b | ||
2×(-
|
解得b=-1,
所以,抛物线的解析式为y=-
| 1 |
| 4 |
∵y=-
| 1 |
| 4 |
| 1 |
| 4 |
∴顶点D的坐标为(-2,4);
(2)令y=0,则-
| 1 |
| 4 |
整理得,x2+4x-12=0,
解得x1=-6,x2=2,
∴点A(-6,0),B(2,0),
如图1,过点D作DE⊥y轴于E,
∵0≤t≤4,
∴△PAD的面积为S=S梯形AOED-S△AOP-S△PDE,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

=-2t+12,
∵k=-2<0,
∴S随t的增大而减小,
∴t=4时,S有最小值,最小值为-2×4+12=4;
(3)如图2,过点D作DF⊥x轴于F,
∵A(-6,0),D(-2,4),
∴AF=-2-(-6)=4,
∴AF=DF,
∴△ADF是等腰直角三角形,
∴∠ADF=45°,
由二次函数对称性,∠BDF=∠ADF=45°,
∴∠PDA=90°时点P为BD与y轴的交点,
∵OF=OB=2,
∴PO为△BDF的中位线,
∴OP=
| 1 |
| 2 |
∴点P的坐标为(0,2),
由勾股定理得,DP=
| (-2-0)2+(4-2)2 |
| 2 |
AD=
| 2 |
| 2 |
∴
| AD |
| DP |
4
| ||
2
|
令x=0,则y=3,
∴点C的坐标为(0,3),OC=3,
∴
| OA |
| OC |
| 6 |
| 3 |
∴
| AD |
| DP |
| OA |
| OC |
又∵∠PDA=90°,∠COA=90°,
∴Rt△ADP∽Rt△AOC.

练习册系列答案
相关题目
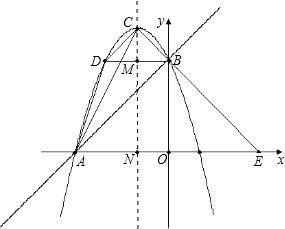 经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.
经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.