题目内容
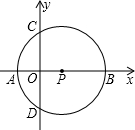
如图,在直角坐标系中,以x轴上一点P(1,0)为圆心的圆与x轴、y轴分别交于A、B、C、D四点,点C的坐标为(0,
).
(1)直接写出A、B、D三点坐标;
(2)若抛物线y=x2+bx+c过A、D两点,求这条抛物线的解析式,并判断点B是否在所求的抛物线上,说明理由.
| 3 |
(1)直接写出A、B、D三点坐标;
(2)若抛物线y=x2+bx+c过A、D两点,求这条抛物线的解析式,并判断点B是否在所求的抛物线上,说明理由.

(1)连接AC、BC,则∠ACB=90°;
∵AB是⊙O的直径,且AB⊥CD,
∴OC=OD;
易知OC=
,则OD=OC=
,即D(0,-
);
Rt△ABC中,OC⊥AB,由射影定理,得:
OA•OB=OC2=3,
设⊙O的半径为R,则OA=R-1,OB=R+1,代入上式,得:
(R+1)(R-1)=3,解得R=2;
∴OA=1,OB=3,即A(-1,0),B(3,0);
所以A、B、D的坐标分别为:A(-1,0),B(3,0),D(0,-
).
(2)将A(-1,0),D(0,-
)代入y=x2+bx+c中,得:
,解得
;
∴y=x2+(1-
)x-
;
当x=3时,x2+(1-
)x-
=9+(1-
)×3-
=12-4
≠0;
∴点B(3,0)不在抛物线y=x2+(1-
)x-
上.
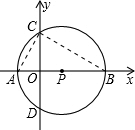
∵AB是⊙O的直径,且AB⊥CD,
∴OC=OD;
易知OC=
| 3 |
| 3 |
| 3 |
Rt△ABC中,OC⊥AB,由射影定理,得:
OA•OB=OC2=3,
设⊙O的半径为R,则OA=R-1,OB=R+1,代入上式,得:
(R+1)(R-1)=3,解得R=2;
∴OA=1,OB=3,即A(-1,0),B(3,0);
所以A、B、D的坐标分别为:A(-1,0),B(3,0),D(0,-
| 3 |
(2)将A(-1,0),D(0,-
| 3 |
|
|
∴y=x2+(1-
| 3 |
| 3 |
当x=3时,x2+(1-
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∴点B(3,0)不在抛物线y=x2+(1-
| 3 |
| 3 |


练习册系列答案
相关题目


 ,动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动.AO1交于轴于点E,设P、Q运动的时间为t秒.
,动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动.AO1交于轴于点E,设P、Q运动的时间为t秒.