题目内容
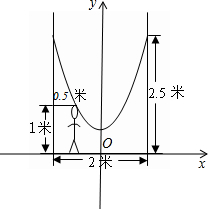
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方 距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,
距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,
(1)选取合适的点作为原点,建立直角坐标系,求出抛物线的解析式;
(2)求绳子的最低点距地面的距离.
 距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,
距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,(1)选取合适的点作为原点,建立直角坐标系,求出抛物线的解析式;
(2)求绳子的最低点距地面的距离.
(1)按要求建立直角坐标系.
设抛物线的函数关系式为:y=ax2+c.
将(-0.5,1)、(1,2.5)代入y=ax2+c得:
,
∴
.
∴绳子所在抛物线的函数关系式为:y=2x2+0.5.
(2)∵当x=0时,y=2x2+0.5=0.5,
∴绳子的最低点离地面的距离为0.5米.
设抛物线的函数关系式为:y=ax2+c.
将(-0.5,1)、(1,2.5)代入y=ax2+c得:
|
∴
|
∴绳子所在抛物线的函数关系式为:y=2x2+0.5.
(2)∵当x=0时,y=2x2+0.5=0.5,
∴绳子的最低点离地面的距离为0.5米.


练习册系列答案
相关题目
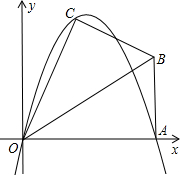 x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.

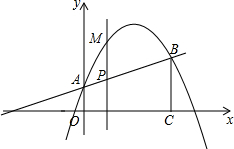
 直线l与x轴平行,O为坐标原点,P、Q为抛物线y=ax2+bx+c(a≠0)上的两动点.
直线l与x轴平行,O为坐标原点,P、Q为抛物线y=ax2+bx+c(a≠0)上的两动点.

