题目内容
如图,已知二次函数y=x2+bx+3与x轴交于点B(3,0),与y轴交于点A,O为坐标原点,P是二次函数y=x2+bx+3 的图象上一个动点,点P的横坐标是m,且m>3,过点P作PM,PM交直线AB于M.
的图象上一个动点,点P的横坐标是m,且m>3,过点P作PM,PM交直线AB于M.
(1)求二次函数的解析式;
(2)若以AB为直径的⊙N恰好与直线PM相切,求此时点M的坐标;
(3)在点P的运动过程中,△APM能否为等腰三角形?若能,求出点P的坐标;若不能请说出理由.
 的图象上一个动点,点P的横坐标是m,且m>3,过点P作PM,PM交直线AB于M.
的图象上一个动点,点P的横坐标是m,且m>3,过点P作PM,PM交直线AB于M.(1)求二次函数的解析式;
(2)若以AB为直径的⊙N恰好与直线PM相切,求此时点M的坐标;
(3)在点P的运动过程中,△APM能否为等腰三角形?若能,求出点P的坐标;若不能请说出理由.
(1)将点B(3,0)坐标代入y=x2+bx+3得:0=9+3b+3,
解得b=-4,
∴二次函数的解析式为y=x2-4x+3;
(2)令x=0,则y=3,∴A点坐标为A(0,3),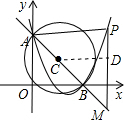
直线AB的解析式为y=-x+3,
C为⊙C的圆心,CA=CB=
,
故C点坐标为(
,
),
过C作CD⊥PM于点D,CD=CA=CB=
,
∴D点坐标为(
(1+
),
),
xM=
(1+
),
将xM=
(1+
)代入y=-x+3得yM=
(1-
),
∴点M的坐标为(
(1+
),
(1-
));
(3)若△APM为等腰三角形,进行分类讨论;
①当PA=PM时,P(m,m2-4m+3)则M(m,-m+3),
|PM|=|m2-3m|,|PA|=
,|AM|=
=m
;
由PA=PM可得|m2-3m|=
,
解得m=4,m2-4m+3=3,
则P点坐标为P(4,3),
②当PA=AM时,
=m
,
解得m=3,或m=5,
当m=3时,m2-4m+3=0,由题意可知m>3,故m=3不合题意;
当m=5时,m2-4m+3=8,
故点P坐标为(5,8),
③当PA=AM时,|m2-3m|=m
,
解得m=3+
或m=3-
,
由题意可知m>3,故m=3-
舍去,
当m=3+
时,m2-4m+3=2
+2,
故点P坐标为(3+
,2+
).
解得b=-4,
∴二次函数的解析式为y=x2-4x+3;
(2)令x=0,则y=3,∴A点坐标为A(0,3),

直线AB的解析式为y=-x+3,
C为⊙C的圆心,CA=CB=
| 3 |
| 2 |
| 2 |
故C点坐标为(
| 3 |
| 2 |
| 3 |
| 2 |
过C作CD⊥PM于点D,CD=CA=CB=
| 3 |
| 2 |
| 2 |
∴D点坐标为(
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
xM=
| 3 |
| 2 |
| 2 |
将xM=
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
∴点M的坐标为(
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
(3)若△APM为等腰三角形,进行分类讨论;
①当PA=PM时,P(m,m2-4m+3)则M(m,-m+3),
|PM|=|m2-3m|,|PA|=
| m2+(m2-4m)2 |
| m2+(3+m-3)2 |
| 2 |
由PA=PM可得|m2-3m|=
| m2+(m2-4m)2 |
解得m=4,m2-4m+3=3,
则P点坐标为P(4,3),
②当PA=AM时,
| m2+(m2-4m)2 |
| 2 |
解得m=3,或m=5,
当m=3时,m2-4m+3=0,由题意可知m>3,故m=3不合题意;
当m=5时,m2-4m+3=8,
故点P坐标为(5,8),
③当PA=AM时,|m2-3m|=m
| 2 |
解得m=3+
| 2 |
| 2 |
由题意可知m>3,故m=3-
| 2 |
当m=3+
| 2 |
| 2 |
故点P坐标为(3+
| 2 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
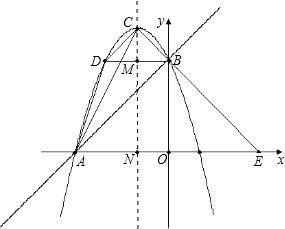 经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.
经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.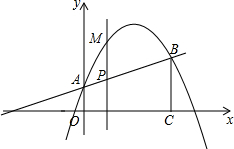
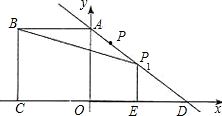 形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由.
形BCEP1的面积为S,请问S是否有最大值?若有,请求出P点坐标和S的最大值;若没有,请说明理由. 且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,
且A点在y轴上,以C为圆心,CA为半径的⊙C与x轴相切,

