题目内容
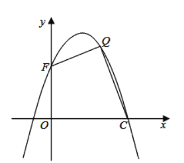
【题目】已知函数y＝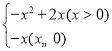
的图象如图所示，若直线y＝x+m与该图象恰有三个不同的交点，则m的取值范围为_____.
【答案】0＜m＜
【解析】
由直线y＝x+m与该图象恰有三个不同的交点可知直线y＝x+m与y=-x(x≤0)有一个交点，与y=-x2+2x有两个交点，分别联立两个解析式求出m的取值范围即可得答案.
∵直线y＝x+m与该图象恰有三个不同的交点，
∴直线y＝x+m与y=-x(x≤0)有一个交点，与y=-x2+2x(x>0)有两个交点，
x+m=-x
x=
，
∵x≤0，
∴m≥0，
-x2+2x=x+m，
x2-x+m=0，
∵y=x+m与y=-x2+2x(x>0)有两个交点，
∴△=(-1)2-4m>0，
解得：m<，
∵当m=0时，直线y=x+m过（0，0）点，
∴与y＝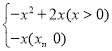
图象只有两个交点，
∴m≠0，
∴m的取值范围为：0＜m＜.
故答案为：0＜m＜
练习册系列答案
相关题目
【题目】已知二次函数y＝﹣x2+bx+c，函数值y与自变量x之间的部分对应值如下表：
x | … | ﹣4 | ﹣1 | 0 | 1 | … |
y | … | ﹣2 | ﹣1 | ﹣2 | ﹣7 | … |
（1）此二次函数图象的对称轴是直线，此函数图象与x轴交点个数为 ．
（2）求二次函数的函数表达式；
（3）当﹣5＜x＜﹣1时，请直接写出函数值y的取值范围．
