题目内容
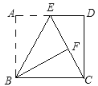
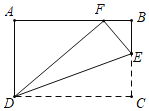
【题目】如图，在矩形ABCD中，AB＝10，AD＝6，E为BC上一点，把△CDE沿DE折叠，使点C落在AB边上的F处，则CE的长为_____．
【答案】
【解析】
设CE＝x，则BE＝6﹣x由折叠性质可知，EF＝CE＝x，DF＝CD＝AB＝10，所以AF＝8，BF＝AB﹣AF＝10﹣8＝2，在Rt△BEF中，BE2+BF2＝EF2，即（6﹣x）2+22＝x2，解得x＝．
解：设CE＝x，则BE＝6﹣x由折叠性质可知，EF＝CE＝x，DF＝CD＝AB＝10，
在Rt△DAF中，AD＝6，DF＝10，
∴AF＝8，
∴BF＝AB﹣AF＝10﹣8＝2，
在Rt△BEF中，BE2+BF2＝EF2，
即（6﹣x）2+22＝x2，
解得x＝，
故答案为．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题：
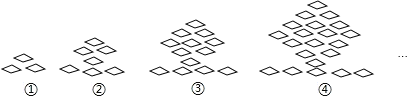
（1）填写下表：
图形序号 | 菱形个数 |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
（2）根据表中规律猜想,图n中菱形的个数
用含n的式子表示,不用说理
；
（3）是否存在一个图形恰好由91个菱形组成？若存在,求出图形的序号；若不存在,说明理由.
