ĢāÄæÄŚČŻ
”¾ĢāÄæ”æĆæÄźµÄÅ©ĄśČżŌĀ³õŅ»ĪŖĶØÖŻ·ēóŻ½Ś£®ÕāĢģ£¬Š”ĮõĶ¬Ń§ÕżŌŚ½ŗ£Ć÷Öé¹ć³”ÉĻ·Å·ēóŻ£¬ČēĶ¼·ēóŻ“ÓA“¦Ęš·É£¬¼ø·ÖÖÓŗó±ć·É“ļC“¦£¬“ĖŹ±£¬ŌŚAQŃÓ³¤ĻßÉĻB“¦µÄŠ”ĖĪĶ¬Ń§£¬·¢ĻÖ×Ō¼ŗµÄĪ»ÖĆÓė·ēóŻŗĶ¹ć³”±ßĘģøĖPQµÄ¶„µćPŌŚĶ¬Ņ»Ö±ĻßÉĻ.
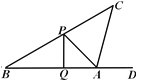
£Ø1£©ŅŃÖŖĘģøĖøßĪŖ10Ć×£¬ČōŌŚB“¦²āµĆĘģøĖ¶„µćPµÄŃö½ĒĪŖ30”ć£¬A“¦²āµĆµćPµÄŃö½ĒĪŖ45”ć£¬ŹŌĒóA”¢BÖ®¼äµÄ¾ąĄė£»
£Ø2£©“ĖŹ±£¬ŌŚA“¦±³ĻņĘģøĖÓÖ²āµĆ·ēóŻµÄŃö½ĒĪŖ75”ć£¬ČōÉž×ÓŌŚæÕÖŠŹÓĪŖŅ»ĢõĻ߶Ī£¬ĒóÉž×ÓACĪŖ¶ąÉŁĆ×£æ£Ø½į¹ūæɱ£ĮōøłŗÅ£©
”¾“š°ø”æ½ā£ŗ£Ø1£©ŌŚRt”÷BPQÖŠ£¬PQ=10Ć×£¬”ĻB=30”ć£¬
ŌņBQ=cot30”ć”ĮPQ£½![]() ,
,
ÓÖŌŚRt”÷APQÖŠ£¬”ĻPAB=45”ć£¬
ŌņAQ=tan45”ć”ĮPQ=10£¬
¼“£ŗAB=£Ø![]() +10£©£ØĆ×£©
+10£©£ØĆ×£©
£Ø2£©¹żA×÷AE”ĶBCÓŚE£¬

ŌŚRt”÷ABEÖŠ£¬”ĻB=30”ć£¬AB=![]() +10£¬
+10£¬
”ą AE=sin30”ć”ĮAB=![]() £Ø
£Ø![]() +10£©=5
+10£©=5![]() +5£¬
+5£¬
”ß”ĻCAD=75”ć£¬”ĻB=30”ć ”ą ”ĻC=45”ć£¬
ŌŚRt”÷CAEÖŠ£¬sin45”ć£½![]() £¬
£¬
”ąAC=![]() £Ø5
£Ø5![]() +5£©=£Ø5
+5£©=£Ø5![]() +5
+5![]() £©£ØĆ×£©
£©£ØĆ×£©
”¾½āĪö”æŹ×ĻČ·ÖĪöĶ¼ŠĪ£ŗøł¾ŻĢāŅā¹¹ŌģÖ±½ĒČż½ĒŠĪ£»±¾ĢāÉę¼°µ½Į½øöÖ±½ĒČż½ĒŠĪ”÷BPQ”¢”÷ABE£¬Ó¦ĄūÓĆPQ=10Ć×¹¹Ōģ·½³Ģ¹ŲĻµŹ½£¬½ų¶ųæɽā¼“æÉĒó³ö“š°ø£®